有一个长度为5 m的梯子贴靠在笔直的墙上,假设其下端沿地板以3 m/s的速度离开墙脚滑动,求当其下端离开墙脚1.4 m时,梯子上端下滑的速度.
已知函数 的图象与函数
的图象与函数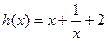 的图象关于点A(0,1)对称.(1)求
的图象关于点A(0,1)对称.(1)求 的解析式;(2)(文)若
的解析式;(2)(文)若 且
且 在区间(0,
在区间(0,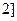 上为减函数,求实数
上为减函数,求实数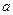 的取值范围; (理)若
的取值范围; (理)若 =
= +
+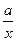 ,且
,且 在区间(0,
在区间(0,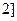 上为减函数,求实数
上为减函数,求实数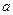 的取值范围.
的取值范围.
设 的定义域为
的定义域为 ,
, 的导函数为
的导函数为 ,且对任意正数
,且对任意正数 均有
均有 ,
,
(1)判断函数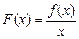 在
在 上的单调性;
上的单调性;
(2)设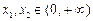 ,比较
,比较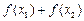 与
与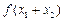 的大小,并证明你的结论;
的大小,并证明你的结论;
(3)设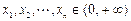 ,若
,若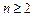 ,比较
,比较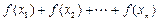 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
已知 R,函数
R,函数 (x∈R).
(x∈R).
(1)当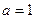 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)函数 是否在R上单调递减,若是,求出
是否在R上单调递减,若是,求出 的取值范围;若不是,请说明理由;
的取值范围;若不是,请说明理由;
(3)若函数 在
在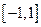 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
已知函数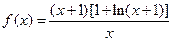 .
.
⑴设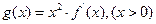 .试证明
.试证明 在区间
在区间 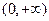 内是增函数;
内是增函数;
⑵若存在唯一实数 使得
使得 成立,求正整数
成立,求正整数 的值;
的值;
⑶若 时,
时,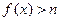 恒成立,求正整数
恒成立,求正整数 的最大值.
的最大值.
已知函数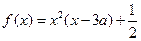 (
(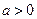 ,
, ).
).
(Ⅰ)求函数 的极值;
的极值; (Ⅱ)若函数
(Ⅱ)若函数 有三个不同的零点,求实数
有三个不同的零点,求实数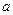 的取值范围.
的取值范围.