在△ABC中,角A,B,C所对的边分别为a,b,c,且满足cos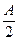 =
=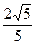 ,
,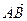 ·
·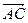 =3,若c=1,求a的值.
=3,若c=1,求a的值.
给出下列命题:
(1)存在实数 ,使sin
,使sin cos
cos =1;(2)存在实数
=1;(2)存在实数 ,使sin
,使sin +cos
+cos =
=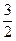 ; (3)y=sin(
; (3)y=sin(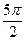 -2x)是偶函数;(4)x=
-2x)是偶函数;(4)x=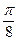 是函数y=
是函数y=  sin(2x+
sin(2x+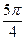 )的一条对称轴的方程;(5)若
)的一条对称轴的方程;(5)若 、
、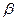 是第一象限角,且
是第一象限角,且
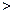
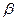 ,则sin
,则sin
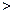 sin
sin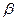 ;其中所有的正确命题的序号是 .
;其中所有的正确命题的序号是 .
如图,函数y=2sin( x+
x+ )(其中x
)(其中x R,0
R,0


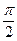 )
)
的图象与y轴交于点(0,1). (1)求 的值; (2)设P是图象
的值; (2)设P是图象
上的最高点,M、N是图象与x轴的交点,求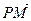 与
与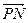 的夹角.
的夹角.
一根杆子长 ,任意地将其折成几段,如果折段点为(1)一个;(2)二个,而且杆子折段在任何位置是等可能的,试求每段杆子的长度均不少于10
,任意地将其折成几段,如果折段点为(1)一个;(2)二个,而且杆子折段在任何位置是等可能的,试求每段杆子的长度均不少于10 的概率。
的概率。
某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
| x |
2 |
4 |
5 |
6 |
8 |
| y |
30 |
40 |
60 |
50 |
70 |
(1)求线性回归方程;
(2)预测当广告费支出7(百万元)时的销售额。
(用最小二乘法求线性回归方程系数公式 )
)