(12分)已知AB是椭圆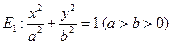 的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点
的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点 . (1)设双曲线E2的离心率为
. (1)设双曲线E2的离心率为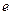 ,求
,求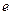 关于
关于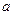 的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.
的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.
某地最近出台一项机动车驾照考试规定:每位考试者一年之内最多有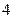 次参加考试的机会,一旦某次考试通过,便可领取驾照,不再参加以后的考试,否则就一直考到第
次参加考试的机会,一旦某次考试通过,便可领取驾照,不再参加以后的考试,否则就一直考到第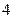 次为止.如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为
次为止.如果李明决定参加驾照考试,设他每次参加考试通过的概率依次为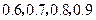 .求在一年内李明参加驾照考试次数
.求在一年内李明参加驾照考试次数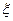 的分布列和
的分布列和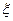 的期望,并求李明在一年内领到驾照的概率.
的期望,并求李明在一年内领到驾照的概率.
已知椭圆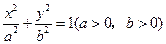 的离心率
的离心率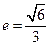 ,过点
,过点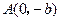 和
和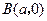 的直线与原点的距离为
的直线与原点的距离为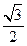 .
.
(1)求椭圆的方程.
(2)已知定点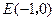 ,若直线
,若直线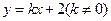 与椭圆交于
与椭圆交于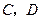 两点,试判断:是否存在
两点,试判断:是否存在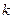 的值,使以
的值,使以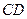 为直径的圆过点
为直径的圆过点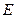 ?若存在,求出这个值;若不存在,说明理由.
?若存在,求出这个值;若不存在,说明理由.
用数学归纳法证明: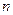 为正偶数时,
为正偶数时,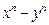 能被
能被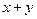 整除.
整除.
经过原点作圆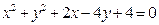 的割线,交圆于
的割线,交圆于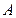 ,
,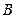 两点,求弦
两点,求弦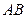 的中点
的中点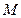 的轨迹方程.
的轨迹方程.
已知函数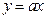 与
与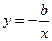 在区间
在区间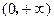 上都是减函数,确定函数
上都是减函数,确定函数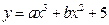 的单调区间.
的单调区间.