如图,四棱锥 中,侧面
中,侧面 是边长为2的正三角形,底面
是边长为2的正三角形,底面 是菱形,
是菱形, ,点
,点 在底面
在底面 上的射影为
上的射影为 的重心,点
的重心,点 为线段
为线段 上的点.
上的点.
(1)当点 为
为 的中点时,求证:
的中点时,求证: 平面
平面 ;
;
(2)当平面 与平面
与平面 所成锐二面角的余弦值为
所成锐二面角的余弦值为 时,求
时,求 的值.
的值.
(本题满分12分)已知函数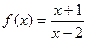 ,
,
(1)判断函数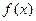 的单调性,并用定义加以证明;(2)求函数
的单调性,并用定义加以证明;(2)求函数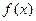 的最大值和最小值
的最大值和最小值
(本题满分12分)设集合A=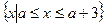 ,集合B={x|x<-1或x>5},分别就下列条件求实数a的取值范围
,集合B={x|x<-1或x>5},分别就下列条件求实数a的取值范围
(1)A∩B≠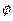 ,(2)A∩B=A.
,(2)A∩B=A.
(本题满分12分)设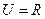 ,
,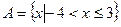 ,
,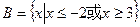 ,求:
,求:
(1)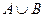 ;(2)
;(2)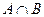 ;(3)
;(3)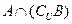
(本小题满分12分) 已知函数 ,数列
,数列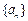 ,
, 满足条件:
满足条件: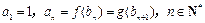 .
.
(1)求证:数列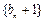 为等比数列;
为等比数列;
(2)令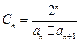 ,Tn是数列
,Tn是数列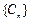 的前n项和,求使
的前n项和,求使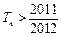 成立的最小的n值.
成立的最小的n值.
(本小题满分12分) 设a > 1,函数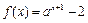 .
.
(1)求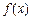 的反函数
的反函数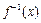 ;
;
(2)若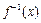 在[0,1]上的最大值与最小值互为相反数,求a的值;
在[0,1]上的最大值与最小值互为相反数,求a的值;
(3)若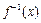 的图象不经过第二象限,求a的取值范围.
的图象不经过第二象限,求a的取值范围.