设椭圆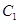 :
: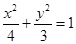 ,
,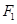 ,
,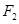 分别是椭圆的左右焦点,过椭圆右焦点
分别是椭圆的左右焦点,过椭圆右焦点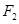 的直线
的直线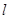 与椭圆
与椭圆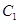 交于
交于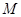 ,
,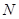 两点.
两点.
(1)是否存在直线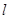 ,使得
,使得 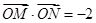 ,若存在,求出直线
,若存在,求出直线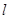 的方程;若不存在,说明理由;
的方程;若不存在,说明理由;
(2)若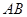 是椭圆
是椭圆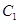 经过原点
经过原点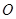 的弦,且
的弦,且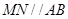 ,求证:
,求证: 为定值.
为定值.
(本小题满分12分)设向量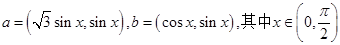 .
.
(1)若向量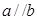 ,求
,求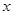 的值;
的值;
(2)设函数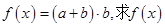 的最大值.
的最大值.
(本小题满分12分)设递增等差数列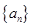 的前n项和为
的前n项和为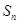 ,已知
,已知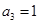 ,
,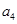 是
是 和
和 的等比中项.
的等比中项.
(l)求数列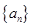 的通项公式;
的通项公式;
(2)求数列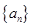 的前n项和
的前n项和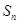
已知函数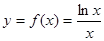 。
。
(Ⅰ)求函数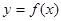 的图像在
的图像在 处的切线方程;
处的切线方程;
(Ⅱ)求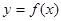 的最大值;
的最大值;
(Ⅲ)设实数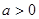 ,求函数
,求函数 在
在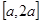 上的最小值
上的最小值
某种商品的成本为5元/ 件,开始按8元/件销售,销售量为50件,为了获得最大利润,商家先后采取了提价与降价两种措施进行试销。经试销发现:日销售量Q(件)与实际销售价x(元)满足关系: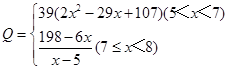
(1)求总利润(利润=销售额-成本)y(元)与销售价x(件)的函数关系式;
(2)试问:当实际销售价为多少元时,总利润最大.
已知数列 的前
的前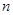 项和
项和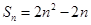 ,数列
,数列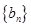 的前
的前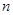 项和
项和 。
。
(Ⅰ)求数列 和
和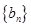 的通项公式;
的通项公式;
(Ⅱ)设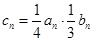 ,求数列
,求数列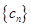 的前
的前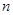 项和
项和 表达式。
表达式。