(本小题满分12分)已知椭圆 的左、右焦点分别为
的左、右焦点分别为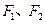 ,离心率
,离心率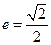 ,右准线方程
,右准线方程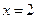 . (1)求椭圆的标准方程;(2)过点
. (1)求椭圆的标准方程;(2)过点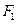 的直线
的直线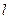 与该椭圆相交于M、N两点,且
与该椭圆相交于M、N两点,且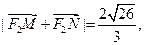 求直线
求直线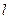 的方程。
的方程。
已知圆 关于
关于 轴对称,经过抛物线
轴对称,经过抛物线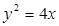 的焦点,且被直线
的焦点,且被直线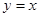 分成两段弧长之比为1∶2,求圆
分成两段弧长之比为1∶2,求圆 的方程.
的方程.
已知命题 :关于
:关于 的一元二次方程
的一元二次方程 没有实数根,命题
没有实数根,命题 :函数
:函数 的定义域为
的定义域为 ,若
,若 或
或 为真命题,
为真命题, 且
且 为假命题,求实数
为假命题,求实数 的取值范围.
的取值范围.
设动点
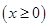 到定点
到定点 的距离比到
的距离比到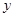 轴的距离大
轴的距离大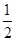 .记点
.记点 的轨迹为曲线
的轨迹为曲线 .
.
(1)求点 的轨迹方程;
的轨迹方程;
(2)设圆 过
过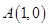 ,且圆心
,且圆心 在
在 的轨迹上,
的轨迹上,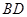 是圆
是圆 在
在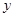 轴上截得的弦,当
轴上截得的弦,当 运动时弦长
运动时弦长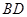 是否为定值?说明理由;
是否为定值?说明理由;
(3)过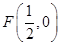 做互相垂直的两直线交曲线
做互相垂直的两直线交曲线 于
于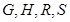 ,求四边形
,求四边形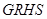 面积的最小值.
面积的最小值.
已知椭圆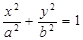
 >
> >
> 与直线
与直线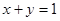 交于
交于 、
、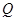 两点,且
两点,且 ,其中
,其中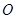 为坐标原点.
为坐标原点.
(1)求 的值;
的值;
(2)若椭圆长轴的取值范围为 ,求椭圆的离心率
,求椭圆的离心率 的取值范围.
的取值范围.
已知双曲线的中心在坐标原点,实轴在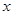 轴上,其离心率
轴上,其离心率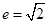 ,已知点
,已知点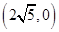 到双曲线上的点的最短距离为
到双曲线上的点的最短距离为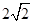 ,求双曲线的方程.
,求双曲线的方程.