已知向量 ,
,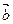 =(1,2).
=(1,2).
(1)若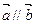 ,求tan
,求tan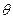 的值; (2)若
的值; (2)若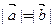 ,
,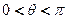 ,求
,求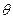 的值.
的值.
某小组共10人,利用假期参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4,. 现从这10人中随机选出2人作为该组代表参加座谈会.
(1)设A为事件“选出的2人参加义工活动次数之和为4”,求事件A发生的概率;
(2)设 为选出的2人参加义工活动次数之差的绝对值,求随机变量 的分布列和数学期望.
已知函数 .
(1)求 的定义域与最小正周期;
(2)讨论f(x)在区间 上的单调性.
已知,椭圆C以过点, ,两个焦点为 。
(Ⅰ)求椭圆C的方程;
(Ⅱ)E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
设 ,且曲线 在 处的切线与x轴平行。
(Ⅰ)求 的值,并讨论 的单调性;
(Ⅱ)证明:当
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表:

(Ⅰ)试分别估计两个分厂生产的零件的优质品率;
(Ⅱ)由于以上统计数据填下面 列联表,并问是否有99%的把握认为"两个分厂生产的零件的质量有差异"。

附: