设 ,且曲线 在 处的切线与x轴平行。
(Ⅰ)求 的值,并讨论 的单调性;
(Ⅱ)证明:当
某校在高二年级开设了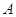 ,
,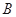 ,
,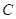 三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从
三个兴趣小组,为了对兴趣小组活动的开展情况进行调查,用分层抽样方法从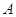 ,
,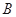 ,
,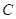 三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
三个兴趣小组的人员中,抽取若干人组成调查小组,有关数据见下表(单位:人)
| 兴趣小组 |
小组人数 |
抽取人数 |
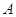 |
12 |
 |
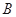 |
36 |
3 |
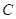 |
48 |
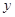 |
(1)求 ,
,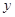 的值;
的值;
(2)若从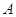 ,
,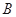 两个兴趣小组所抽取的人中选2人作专题发言,求这2人都来自兴趣小组
两个兴趣小组所抽取的人中选2人作专题发言,求这2人都来自兴趣小组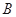 的概率.
的概率.
已知函数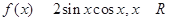 .
.
(1)求函数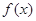 的最小正周期;
的最小正周期;
(2)判断函数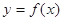 的奇偶性, 并说明理由。
的奇偶性, 并说明理由。
我们把一系列向量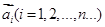 排成一列,称为向量列,记作
排成一列,称为向量列,记作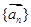 ,又设
,又设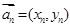 ,假设向量列
,假设向量列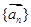 满足:
满足: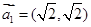 ,
,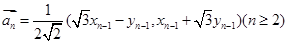 。
。
(1)证明数列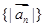 是等比数列;
是等比数列;
(2)设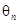 表示向量
表示向量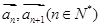 间的夹角,若
间的夹角,若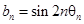 ,记
,记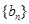 的前
的前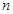 项和为
项和为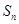 ,求
,求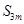 ;
;
(3)设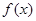 是
是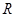 上不恒为零的函数,且对任意的
上不恒为零的函数,且对任意的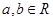 ,都有
,都有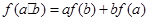 ,若
,若 ,
,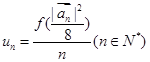 ,求数列
,求数列 的前
的前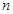 项和
项和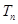 .
.
已知数列 的各项均为正数,其前
的各项均为正数,其前 项和为
项和为 ,且
,且 ,
, ,数列
,数列 是首项和公比均为
是首项和公比均为 的等比数列.
的等比数列.
(1)求证数列 是等差数列;
是等差数列;
(2)若 ,求数列
,求数列 的前
的前 项和
项和 .
.
在 中,内角
中,内角 对边的长分别是
对边的长分别是 ,且
,且 .
.
(1)若 的面积等于
的面积等于 ,求
,求 ;
;
(2)若 ,求
,求 的面积.
的面积.