(本小题满分12分)已知函数 在区间
在区间 上为增函数,求实数
上为增函数,求实数 与
与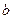 的关系,并证明你的结论。
的关系,并证明你的结论。
(本小题满分14分)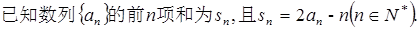
(本小题满分14分)已知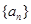 是首项为19,公差d=-2的等差数列,
是首项为19,公差d=-2的等差数列,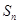 为
为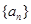 的前n项和.(1)求通项公式
的前n项和.(1)求通项公式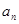 及
及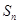 ;
;
(2)设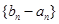 是首项为1,公比为3的等比数列,求数列
是首项为1,公比为3的等比数列,求数列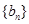 的通项公式及其前n项和
的通项公式及其前n项和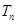
(本小题满分12分) 
(1)求b的值
(2)求sinC的值
(本小题共12分)已知函数 .
.
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)求 在区间
在区间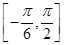 上的最大值和最小值.
上的最大值和最小值.
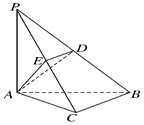
(本小题满分14分).如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC的中点,且DE∥BC.
(1)求证:DE∥平面ACD
(2)求证:BC⊥平面PAC;
(3)求AD与平面PAC所成的角的正弦值;