(本小题满分10分)选修4-5:不等式选讲
已知函数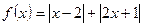 .
.
(Ⅰ) 画出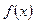 的图象,并写出函数
的图象,并写出函数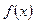 的值域;
的值域;
(Ⅱ) 若关于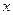 的不等式
的不等式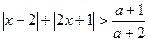 对于任意
对于任意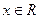 恒成立,求实数
恒成立,求实数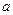
的取值范围.
已知二次函数y=f(x)的图像经过坐标原点,其导函数为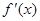 =6x-2,数列{
=6x-2,数列{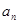 }的前n项和为
}的前n项和为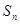 ,点(n,
,点(n,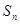 )(n∈N*)均在函数y=f(x)的图像上.(Ⅰ)求数列{
)(n∈N*)均在函数y=f(x)的图像上.(Ⅰ)求数列{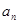 }的通项公式;
}的通项公式;
(Ⅱ)设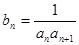 ,
,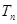 是数列{
是数列{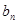 }的前n项和,求使得
}的前n项和,求使得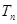 <对所有
<对所有
n∈N*都成立的最小正整数m;
已知函数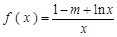 ,
,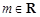 .
.
(Ⅰ)求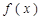 的极值;
的极值;
(Ⅱ)若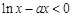 在
在 上恒成立,求
上恒成立,求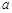 的取值范围.
的取值范围.
某商品每件成本9元,售价为30元,每星期卖出432件,如果降低价格,销售量可以增加,且每星期多卖出的商品件数与商品单价的降低值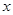 (单位:元,
(单位:元,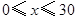 )的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
)的平方成正比,已知商品单价降低2元时,一星期多卖出24件.
(I)将一个星期的商品销售利润表示成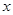 的函数;
的函数;
(II)如何定价才能使一个星期的商品销售利润最大?
数列{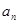 }满足
}满足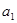 =1,
=1, =
=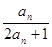 ,(1)计算
,(1)计算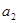 ,
, ,
,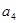 的值;
的值;
(2)归纳推测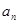 ,并用数学归纳法证明你的推测.
,并用数学归纳法证明你的推测.
已知函数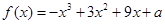
(1)求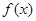 的单调递减区间;
的单调递减区间;
(2)若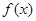 在区间
在区间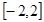 上的最大值为20,求它在该区间上的最小值。
上的最大值为20,求它在该区间上的最小值。