(本小题满分12分) 海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天从0时至24时的时间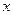 (单位:时)与水深y(单位:米)的关系表:
(单位:时)与水深y(单位:米)的关系表:
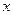 |
0:00 |
3:00 |
6:00 |
9: 00 |
12:00 |
15:00 |
18:00 |
21:00 |
24:00 |
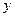 |
12.0 |
15.0 |
12.0 |
9.0 |
12.0 |
15.0 |
12.0 |
9.0 |
12.0 |
(1)请选用一个函数来近似描述这个港口的水深与时间的函数关系;
(2)一条货轮的吃水深度(船体最低点与水面的距离)为12米,安全条例规定船体最低点与
洋底间隙至少要有1.5米,请问该船何时能进出港口?在港口最多能停留多长时间?
(本小题满分14分)设椭圆
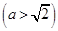 的右焦点为
的右焦点为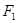 ,直线
,直线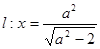 与
与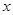 轴交于点
轴交于点 ,若
,若 (其中
(其中 为坐标原点).
为坐标原点).
(1)求椭圆 的方程;
的方程;
(2)设 是椭圆
是椭圆 上的任意一点,
上的任意一点,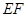 为圆
为圆 的任意一条直径(
的任意一条直径( 、
、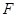 为直径的两个端点),求
为直径的两个端点),求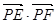 的最大值.
的最大值.
(本小题满分14分)如图所示,已知正方形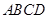 的边长为2,
的边长为2, .将正方形
.将正方形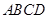 沿对角线
沿对角线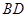 折起,得到三棱锥
折起,得到三棱锥 .
.
(1)求证:平面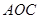
 平面
平面 ;
;
(2)若三棱锥 的体积为
的体积为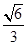 ,求
,求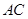 的长.
的长.
(本小题满分14分)各项均为正数的数列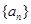 ,满足
,满足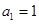 ,
,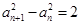 (
( ).
).
(1)求数列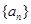 的通项公式;
的通项公式;
(2)求数列 的前
的前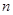 项和
项和 .
.
(本小题满分12分)某城市为准备参加“全国文明城市”的评选,举办了“文明社区”评选的活动,在第一轮暗访评分中,评委会对全市50个社区分别从“居民素质”和“社区服务”两项进行评分,每项评分均采用5分制,若设“社区服务”得分为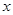 分,“居民素质”得分为
分,“居民素质”得分为 分,统计结果如下表:
分,统计结果如下表:
(1)若“居民素质”得分和“社区服务”得分均不低于3分(即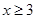 且
且 )的社区可以进入第二轮评比,现从50个社区中随机选取一个社区,求这个社区能进入第二轮评比的概率;
)的社区可以进入第二轮评比,现从50个社区中随机选取一个社区,求这个社区能进入第二轮评比的概率;
(2)若在50个社区中随机选取一个社区,这个社区的“居民素质”得1分的概率为 ,求
,求 、
、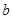 的值.
的值.
(本小题满分12分)如图,在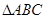 中,点
中,点 在
在 边上,
边上,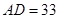 ,
, ,
,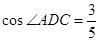 .
.
(1)求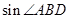 的值;
的值;
(2)求 的长.
的长.