已知点 ,
, 分
分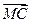 所成的比为2,
所成的比为2,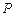 是平面上一动点,且满足
是平面上一动点,且满足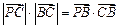 .(1)求点
.(1)求点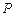 的轨迹
的轨迹 对应的方程;(2) 已知点
对应的方程;(2) 已知点 在曲线
在曲线 上,过点
上,过点 作曲线
作曲线 的两条弦
的两条弦 ,且直线
,且直线 的斜率
的斜率 满足
满足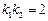 ,试推断:动直线
,试推断:动直线 有何变化规律,证明你的结论.
有何变化规律,证明你的结论.
已知等差数列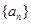 的前
的前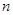 项和为
项和为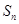 ,且
,且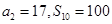 .
.
(I)求数列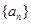 的通项公式;
的通项公式;
(II)若数列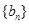 满足
满足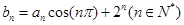 ,求数列
,求数列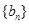 的前
的前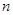 项和.
项和.
某小区要建一座八边形的休闲小区,如右图它在主体造型的平面图是由两个相同的矩形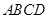 和
和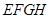 构成的面积为200平方米的十字形地域。计划在正方形
构成的面积为200平方米的十字形地域。计划在正方形 上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
上建一座花坛,造价每平方米4200元,并在四周的四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为每平方米210元,再在四个空角上铺草坪,造价为每平方米80元。
⑴设总造价为 元,
元, 长为
长为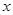 米,试求
米,试求 关于
关于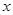 的函数关系式;
的函数关系式;
⑵当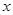 为何值,
为何值, 取得最小值?并求出这个最小值.
取得最小值?并求出这个最小值.
如图,已知点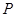 在圆柱
在圆柱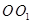 的底面圆
的底面圆 上,
上,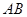 为圆
为圆 的直径,圆柱
的直径,圆柱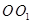 的表面积为
的表面积为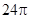 ,
, ,
, 。
。
(1)求三棱锥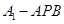 的体积。
的体积。
(2)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;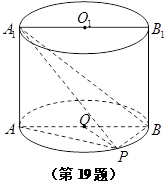
 中内角
中内角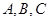 的对边分别为
的对边分别为 ,向量
,向量 且
且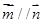 (1)求锐角
(1)求锐角 的大小;(2)如果
的大小;(2)如果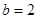 ,求
,求 的面积
的面积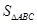 的最大值
的最大值
如图,在四棱锥P—ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,PA=AB=4,
G为PD中点,E点在AB上,平面PEC⊥平面PDC.
(Ⅰ)求证:AG⊥平面PCD;
(Ⅱ)求证:AG∥平面PEC;
(Ⅲ)求点G到平面PEC的距离.