(本小题满分14分)直棱柱 中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,
中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,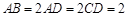 .
.
(1)求证:AC⊥平面BB1C1C;
(2)在A1B1上是否存一点P,使得DP与平面BCB1与平面ACB1都平行?证明你的结论.
已知(1+x)2n=a0+a1x+a2x2+ +a2nx2n.
(1)求a1+a2+a3+ +a2n的值;
(2)求 的值.
的值.
如图所示的几何体 中,
中,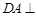 平面
平面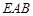 ,
, ∥
∥ ,
, ,
, ,
, 是
是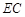 的中点.
的中点.
(1)求证: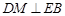 ;
;
(2)求二面角 的余弦值.
的余弦值.
选修4—5:不等式选讲
解不等式:
选修4—4:坐标系与参数方程
已知曲线C:3x2+4y2-6=0(y≥0).
(Ⅰ)写出曲线C的参数方程;
(Ⅱ)若动点P(x,y)在曲线C上,求z=x+2y的最大值与最小值.