给定锐角三角形PBC,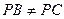 .设A,D分别是边PB,PC上的点,连接AC,BD,相交于点O. 过点O分别作OE⊥AB,OF⊥CD,垂足分别为E,F,线段BC,AD的中点分别为M,N.(1)若A,B,C,D四点共圆,求证:
.设A,D分别是边PB,PC上的点,连接AC,BD,相交于点O. 过点O分别作OE⊥AB,OF⊥CD,垂足分别为E,F,线段BC,AD的中点分别为M,N.(1)若A,B,C,D四点共圆,求证: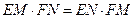 ;
;
(2)若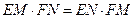 ,是否一定有A,B,C,D四点共圆?证明你的结论.
,是否一定有A,B,C,D四点共圆?证明你的结论.
在周长为 的△
的△ 中,
中, ,求
,求 的取值范围
的取值范围
某汽车城销售某种型号的汽车,每辆进货价为25万元,市场调研表明:当销售价为流程图的输出结果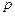 万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价
万元时,平均每周能售出8辆,而当销售价每降低0.5万元时,平均每周能多售出4辆.如果设每辆汽车降价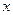 万元,每辆汽车的销售利润为
万元,每辆汽车的销售利润为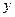 万元.(销售利润
万元.(销售利润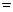 销售价
销售价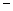 进货价)
进货价)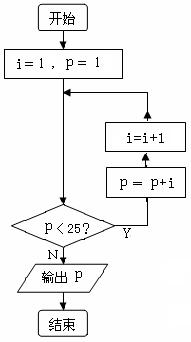

(1)求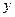 与
与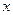 的函数关系式;在保证商家不亏本的前提下,写出
的函数关系式;在保证商家不亏本的前提下,写出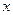 的取值范围;
的取值范围;
(2)假设这种汽车平均每周的销售利润为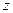 万元,试写出
万元,试写出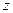 与
与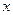 之间的函数关系式;
之间的函数关系式;
(3)当每辆汽车的定价为多少万元时,平均每周的销售利润最大?最大利润是多少?
已知复平面内平行四边形ABCD,点A 对应的复数为 向量
向量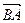 对应的复数为
对应的复数为 向量
向量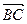 对应的复数为
对应的复数为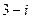
(1)求点C,D对应的复数;
(2)求平行四边形ABCD的面积.
用三段论证明: 通项公式 的数列
的数列 是等差数列.
是等差数列.
某企业人力资源部为了研究企业员工工作积极性和对待企业改革的关系,随机抽取了189 名员工进行调查,其中支持企业改革的被调查者中,工作积极的54人,工作一般的32人,而不太赞成企业改革的被调查者中,工作积极的40人,工作一般的63人, 根据以上数据建立一个2×2的列联表;
名员工进行调查,其中支持企业改革的被调查者中,工作积极的54人,工作一般的32人,而不太赞成企业改革的被调查者中,工作积极的40人,工作一般的63人, 根据以上数据建立一个2×2的列联表;