已知 时的极值为0.
时的极值为0.
(1)求常数a,b的值;
(2)求 的单调区间.
的单调区间.
已知M(0,-2),点A在x轴上,点B在y轴的正半轴,点P在直线AB上,且满足=,·=0.
(1)当点A在x轴上移动时,求动点P的轨迹C的方程;
(2)过(-2,0)的直线l与轨迹C交于E、F两点,又过E、F作轨迹C的切线l1、l2,当l1⊥l2,求直线l的方程.
如右图所示,设抛物线方程为x2=2py(p>0),M为直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A、B.
(1)求证:A、M、B三点的横坐标成等差数列;
(2)已知当M点的坐标为(2,-2p)时,=4,求此时抛物线的方程;
如右图所示,已知四边形ABCD为直角梯形,AD∥BC,∠ABC=90°,PA⊥平面AC,且PA=AD=AB=1,BC=2.
(1)求PC的长;
(2)求异面直线PC与BD所成角的余弦值的大小
如右图所示,在三棱锥A-BCD中,E,F,G,H分别是边AB,BC,CD,DA的中点.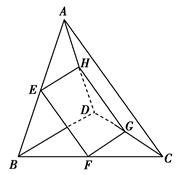
(1)求证:四边形EFGH是平行四边形;
(2)若AC=BD,求证:四边形EFGH是菱形;
(3)当AC与BD满足什么条件时,四边形EFGH是正方形
如右图所示,在四棱锥P—ABCD中,底面ABCD是矩形,PA⊥底面ABCD,PA=AB=1,AD=,点F是PB的中点,点E在边BC上移动.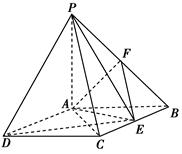
(1)求三棱锥E—PAD的体积;
(2)当点E为BC的中点时,试判断EF与平面PAC的位置关系,并说明理由;
(3)证明:无论点E在边BC的何处,都有PE⊥AF.