设m,n是给定的整数,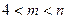 ,
,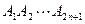 是一个正2n+1边形,
是一个正2n+1边形,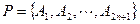 .求顶点属于P且恰有两个内角是锐角的凸m边形的个数.
.求顶点属于P且恰有两个内角是锐角的凸m边形的个数.
已知函数 .
.
(1)若关于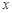 的方程
的方程 只有一个实数解,求实数
只有一个实数解,求实数 的取值范围;
的取值范围;
(2)若当 时,不等式
时,不等式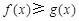 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
(本小题满分16分)
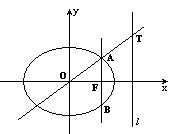
如图,椭圆 的右焦点为
的右焦点为 ,右准线为
,右准线为 ,
,
(1)求到点 和直线
和直线 的距离相等的点
的距离相等的点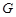 的轨迹方程。
的轨迹方程。
(2)过点 作直线交椭圆
作直线交椭圆 于点
于点 ,又直线
,又直线 交
交 于点
于点 ,若
,若 ,
,
求线段 的长;
的长;
(3)已知点 的坐标为
的坐标为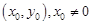 ,直线
,直线 交直线
交直线 于点
于点 ,且和椭圆
,且和椭圆 的一个交点为点
的一个交点为点 ,是否存在实数
,是否存在实数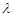 ,使得
,使得 ,若存在,求出实数
,若存在,求出实数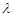 ;若不存在,请说明理由。
;若不存在,请说明理由。
(本小题满分14分)
为了解学生升高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
(Ⅰ)估计该校男生的人数;
(Ⅱ)估计该校学生身高在170~185cm之间的概率;
(Ⅲ)从样本中身高在165~180cm之间的女生中任选2人,求至少有1人身高在170~18cm之间的概率。
如图,在四棱锥 中,底面
中,底面 为矩形,平面
为矩形,平面 ⊥平面
⊥平面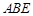 ,
, ,
,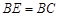 ,
,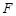 为
为 的中点,
的中点,
求证:(1) ∥平面
∥平面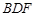 ;(2)平面
;(2)平面 平面
平面 .
.
已知向量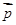 =(
=( ,
, ),
), =(
=(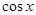 ,
,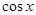 ),定义函数
),定义函数 =
=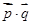
(1)求 的最小正周期
的最小正周期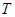 ;
;
(2)若△ 的三边长
的三边长 成等比数列,且
成等比数列,且 ,求边
,求边 所对角
所对角 以及
以及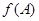 的大小。
的大小。