若公共汽车门的高度是按照保证成年男子与车门顶部碰头的概率在1%以下设计的,如果某地成年男子的身高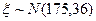 (单位:㎝),则该地公共汽车门的高度应设计为多高?
(单位:㎝),则该地公共汽车门的高度应设计为多高?
从6名短跑运动员中选出4人参加4×100 m接力赛.试求满足下列条件的参赛方案各有多少种?
(1)甲不能跑第一棒和第四棒;
(2)甲不能跑第一棒,乙不能跑第四棒
已知曲线 y = x3 + x-2 在点 P0 处的切线 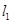 平行直线
平行直线
4x-y-1=0,且点 P0 在第三象限,
求P0的坐标; ⑵若直线 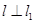 , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.
已知(1+2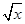 )n的展开式中,某一项的系数恰好是它前一项系数的2倍,而且是它后一项系数的
)n的展开式中,某一项的系数恰好是它前一项系数的2倍,而且是它后一项系数的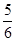 ,求展开式中二项式系数最大的项.
,求展开式中二项式系数最大的项.
一物体沿直线以速度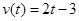 (
( 的单位为:秒,
的单位为:秒,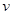 的单位为:米/秒)的速度作变速直线运动,求该物体从时刻t=0秒至时刻 t=5秒间运动的路程?
的单位为:米/秒)的速度作变速直线运动,求该物体从时刻t=0秒至时刻 t=5秒间运动的路程?
设函数f(x)=x+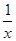 的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x).
的图象为C1,C1关于点A(2,1)对称的图象为C2,C2对应的函数为g(x).
(1)求g(x)的解析式;
(2)若直线y=m与C2只有一个交点,求m的值和交点坐标.