直线 过点
过点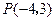 ,与
,与 轴、
轴、 轴分别交于
轴分别交于 两点,并且有向线段
两点,并且有向线段 ,求直线
,求直线 的方程.
的方程.
选修4-2:矩阵与变换(本小题满分10分)
已知矩阵M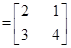
(1)求矩阵M的逆矩阵;
(2)求矩阵M的特征值及特征向量;
选修4-1:几何证明选讲(本小题满分10分)
如图, 半径分别为R,r(R>r>0)的两圆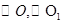 内切于点T,P是外圆
内切于点T,P是外圆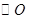 上任意一点,连PT交
上任意一点,连PT交 于点M,PN与内圆
于点M,PN与内圆 相切,切点为N。求证:PN:PM为定值。
相切,切点为N。求证:PN:PM为定值。
(本小题满分16分)
数列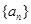 的前n项和为
的前n项和为 ,存在常数A,B,C,使得
,存在常数A,B,C,使得 对任意正整数n都成立。
对任意正整数n都成立。
(1)若数列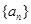 为等差数列,求证:3A-B+C=0;
为等差数列,求证:3A-B+C=0;
(2)若 设
设 数列
数列 的前n项和为
的前n项和为 ,求
,求 ;
;
(3)若C=0,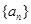 是首项为1的等差数列,设
是首项为1的等差数列,设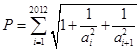 ,求不超过P的最大整数的值。
,求不超过P的最大整数的值。
(本小题满分16分)
已知函数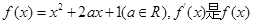 的导函数。
的导函数。
(1)若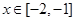 ,不等式
,不等式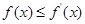 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(2)解关于x的方程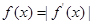 ;
;
(3)设函数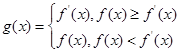 ,求
,求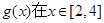 时的最小值;
时的最小值;
(本小题满分16分)
如图,在平面直角坐标系xoy中,圆C: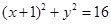 ,点F(1,0),E是圆C上的一个动点,EF的垂直平分线PQ与CE交于点B,与EF交于点D。
,点F(1,0),E是圆C上的一个动点,EF的垂直平分线PQ与CE交于点B,与EF交于点D。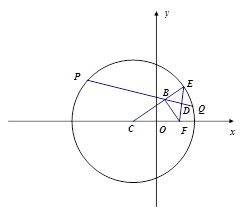
(1)求点B的轨迹方程;
(2)当D位于y轴的正半轴上时,求直线PQ的方程;
(3)若G是圆上的另一个动点,且满足FG⊥FE。记线段EG的中点为M,试判断线段OM的长度是否为定值?若是,求出该定值;若不是,说明理由。