（本小题满分16分）
如图，在平面直角坐标系xoy中，圆C：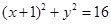
，点F（1，0），E是圆C上的一个动点，EF的垂直平分线PQ与CE交于点B，与EF交于点D。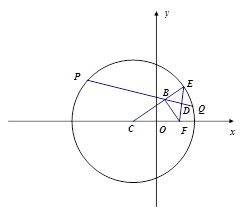
（１） 求点B的轨迹方程；
（２） 当D位于ｙ轴的正半轴上时，求直线PQ的方程；
（３） 若G是圆上的另一个动点，且满足FG⊥FE。记线段EG的中点为M，试判断线段OM的长度是否为定值？若是，求出该定值;若不是，说明理由。
设双曲线C：
（a>0，b>0）的一个焦点坐标为（
，0），离心率
， A、B是双曲线上的两点，AB的中点M（1，2）．
（1）求双曲线C的方程；
（2）求直线AB方程；
（3）如果线段AB的垂直平分线与双曲线交于C、D两点，那么A、B、C、D四点是否共圆？为什么？
已知数列
的前
项和为
，且满足
．
（1）求
，
的值；
（2）求
；
（3）设
，数列
的前
项和为
，求证：
．
如图所示，平面
平面
，且四边形为矩形，四边形为直角梯形，
，
，
，
．
（1）求证
平面
；
（2）求平面
与平面
所成锐二面角的余弦值；
（3）求直线
与平面所成角的余弦值．
已知数列
的前
项和
满足：
，且
（1）求
（2）猜想的通项公式，并用数学归纳法证明
已知函数
的图像经过点
．
（1）求
的值；
（2）在
中，
、
、
所对的边分别为
、
、
，若
，且
．求
．