已知空间四边形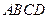 的两条对角线的长
的两条对角线的长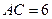 ,
,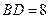 ,
, 与
与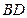 所成的角为
所成的角为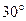 ,
,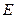 ,
,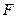 ,
,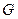 ,
,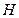 分别是
分别是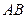 ,
,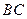 ,
,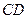 ,
,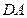 的中点,求四边形
的中点,求四边形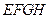 的面积
的面积
已知抛物线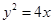 ,作斜率为1的直线
,作斜率为1的直线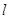 交抛物线于
交抛物线于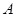 ,
,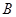 两点,交
两点,交 轴于点
轴于点 ,弦
,弦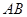 的中点为
的中点为 .
.
(1)若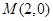 ,求以线段
,求以线段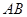 为直径的圆的方程;
为直径的圆的方程;
(2)设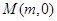 ,若点
,若点 满足
满足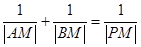 ,求
,求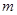 的值.
的值.
已知双曲线的中心在原点,对称轴为坐标轴,一条渐近线为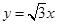 ,右焦点
,右焦点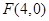 ,左右顶点分别为
,左右顶点分别为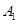 ,
, ,
,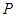 为双曲线上一点(不同于
为双曲线上一点(不同于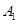 ,
, ),直线
),直线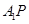 ,
,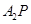 分别与直线
分别与直线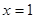 交于
交于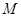 ,
, 两点;
两点;
(1)求双曲线的方程;
(2)求证: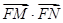 为定值,并求此定值.
为定值,并求此定值.
已知复数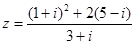 .
.
(1)求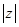 ;
;
(2)若 ,求实数
,求实数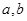 的值.
的值.
【附加题】(5分,计入总分,但总分不超过100分):B班同学做,A班做了也没分L
求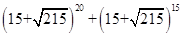 的十进制表达式中的个位数字.
的十进制表达式中的个位数字.
【附加题】(5分,计入总分,但总分不超过100分):A班同学做,B班做了也没分L
设三角形的三边长分别是整数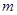 ,
,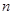 ,
,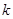 ,且
,且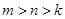 ,已知
,已知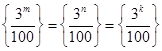 ,其中
,其中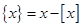 ,而
,而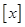 表示不超过
表示不超过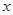 的最大整数,求这种三角形周长的最小值.
的最大整数,求这种三角形周长的最小值.