若函数 在区间
在区间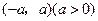 内为偶函数且可导,试讨论
内为偶函数且可导,试讨论 在
在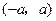 内的奇偶性.
内的奇偶性.
若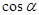 =
= ,
, 是第四象限角,求
是第四象限角,求 的值.
的值.
已知曲线E上的点到直线 的距离比到点F(0,1)的距离大1
的距离比到点F(0,1)的距离大1
(1)求曲线E的方程;
(2)若过M(1,4)作曲线E的弦AB,使弦AB以M为中点,求弦AB所在直线的方程.
(3)若直线 与曲线E相切于点P,求以点P为圆心,且与曲线E的准线相切的圆的方程.
与曲线E相切于点P,求以点P为圆心,且与曲线E的准线相切的圆的方程.
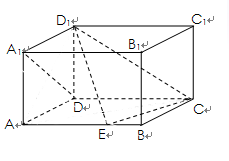
如图,在长方体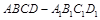 中,
中,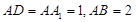 ,点
,点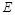 在棱AB上移动.
在棱AB上移动.
(1)证明: ;
;
(2)若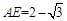 ,求二面角
,求二面角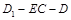 的大小。
的大小。
(本小题满分14分)设函数f(x)=ln x+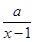 在(e,+∞)内有极值.
在(e,+∞)内有极值.
(Ⅰ)求实数a的取值范围;
(Ⅱ)记g(x)=f(x)+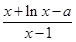 ,判断g(x)的导函数g'(x)在定义域内的单调性;
,判断g(x)的导函数g'(x)在定义域内的单调性;
(Ⅲ)若k<f(x)+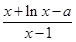 对任意x>1恒成立,求整数k的最大值
对任意x>1恒成立,求整数k的最大值
(本小题满分13分)已知椭圆 过点
过点 ,且与抛物线
,且与抛物线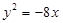 有一个公共的焦点.
有一个公共的焦点.
(Ⅰ)求椭圆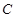 方程;
方程;
(Ⅱ)过椭圆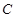 的右焦点
的右焦点 且斜率为
且斜率为 的直线
的直线 与椭圆
与椭圆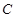 交于
交于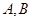 两点,求弦
两点,求弦 的长;
的长;
(Ⅲ)以第(Ⅱ)题中的 为边作一个等边三角形
为边作一个等边三角形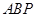 ,求点
,求点 的坐标.
的坐标.