已知抛物线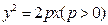 的焦点为
的焦点为 是抛物线上横坐标为
是抛物线上横坐标为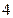 ,且位于
,且位于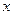 轴上方的点,
轴上方的点, 到抛物线准线的距离等于
到抛物线准线的距离等于 .过
.过 作
作 垂直于
垂直于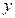 轴,垂足为
轴,垂足为 ,
, 的中点为
的中点为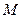 .
.
(1)  求抛物线方程;
求抛物线方程;
(2) 过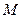 作
作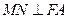 ,垂足为
,垂足为 ,求点
,求点 的坐标;
的坐标;
(3) 以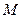 为圆心,
为圆心, 为半径作圆
为半径作圆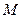 .当
.当 是
是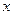 轴上一动点
轴上一动点
时,讨论直线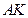 与圆
与圆 的位置关系.
的位置关系.
已知 分别为 三个内角 的对边,
(1)求
(2)若 , 的面积为 ,求 .
数列 满足:
(I)证明:数列 是单调递减数列的充分必要条件是
(II)求 的取值范围,使数列 是单调递增数列。
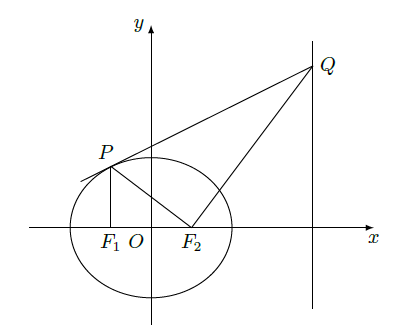
如图,
分别是椭圆
的左,右焦点,过点
作
轴的垂线交椭圆的上半部分于点P,过点
作直线
的垂线交直线
于点
;
(I)若点
的坐标为(4,4);求椭圆
的方程;
(II)证明:直线
与椭圆
只有一个交点
.
设 .
(I)求
在
上的最小值;
(II)设曲线
在点
的切线方程为
;求
的值.
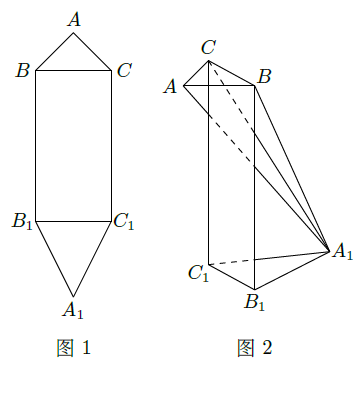
平面图形
如图所示,其中
是矩形,
,
,
。现将该平面图形分别沿
和
折叠,使
与
所在平面都与平面
垂直,再分别连接
,得到如图2所示的空间图形,对此空间图形解答下列问题
(Ⅰ)证明:
;
(Ⅱ)求
的长;
(Ⅲ)求二面角
的余弦值.