(2009四川卷理)(本小题满分12分)
为振兴旅游业,四川省2009年面向国内发行总量为2000万张的熊猫优惠卡,向省外人士发行的是熊猫金卡(简称金卡),向省内人士发行的是熊猫银卡(简称银卡)。某旅游公司组织了一个有36名游客的旅游团到四川名胜旅游,其中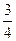 是省外游客,其余是省内游客。在省外游客中有
是省外游客,其余是省内游客。在省外游客中有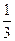 持金卡,在省内游客中有
持金卡,在省内游客中有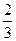 持银卡。
持银卡。

(I)在该团中随机采访3名游客,求恰有1人持金卡且持银卡者少于2人的概率;
(II)在该团的省内游客中随机采访3名游客,设其中持银卡人数为随机变量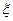 ,求
,求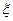 的分布列及数学期望
的分布列及数学期望 。
。
(文科)(本题满分14分)设函数f(x)= ·
· ,其中
,其中 =(m,cos2x),
=(m,cos2x), =(1+sin2x,1),x∈R,且函数y=f(x)的图象经过点(
=(1+sin2x,1),x∈R,且函数y=f(x)的图象经过点( ,2).
,2).
(Ⅰ)求实数m的值;
(Ⅱ)求函数f(x)的最小值及此时x值的集合
(理科)(本题满分14分)已 知函数f(x)=ex-kx,x∈R
知函数f(x)=ex-kx,x∈R
(Ⅰ)若k=e,试确定函数f(x)的单调区间
(Ⅱ)若k>0,且对于任意x∈R,f(|x|)>0恒成立,试确定实数k的取值范围
(本题满分14分)数列{an}中,a1=2,an+1=an+cn(c是常数,n=1,2,3,…),且a1,a2,a3成公比不为1的等比数列
(Ⅰ)求c的值
(Ⅱ)求{an}的通项公式
(本题满分14分)已知集合A={x|x2-2x-3≤0,x∈R},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}
(Ⅰ)若A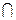 B=[0,3],求实数m的值
B=[0,3],求实数m的值
(Ⅱ)若A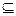 CRB,求实数m的取值范围
CRB,求实数m的取值范围
( 12分)如图,圆柱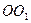 内有一个三棱柱
内有一个三棱柱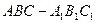 ,三棱柱的底面为圆柱底面的内接三角形,且
,三棱柱的底面为圆柱底面的内接三角形,且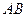 是圆
是圆 的直径。
的直径。
(1)求证:平面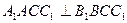
(2)设 ,在圆柱
,在圆柱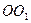 内随机选取一个点,记该点取自三棱
内随机选取一个点,记该点取自三棱
柱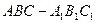 的概率为
的概率为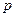
(i)当点C在圆周上运动时,求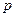 的最大值;
的最大值;
(ii)记平面 与平面
与平面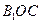 所成的角为
所成的角为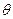
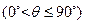 ,当
,当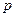
取最大值时,求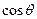 的值。
的值。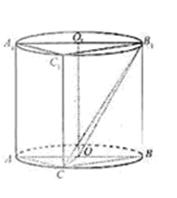
如图,在三棱柱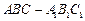
 中,已知
中,已知
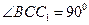 ,
,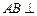 侧面
侧面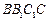 .
.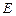 为棱
为棱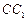 的中点,
的中点,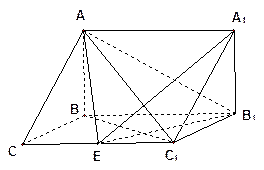
(1)求证: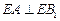 ;(2)若
;(2)若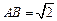 ,求二面角
,求二面角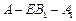 的大小.
的大小.