(本小题满分14分)已知数列{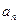 }中,
}中,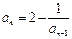 (n≥2,
(n≥2,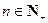 ),
),
(1)若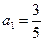 ,数列
,数列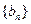 满足
满足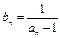 (
(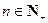 ),求证数列{
),求证数列{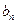 }是等差数列;
}是等差数列;
(2)若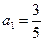 ,求数列{
,求数列{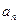 }中的最大项与最小项,并说明理由;
}中的最大项与最小项,并说明理由;
(3)(理做文不做)若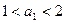 ,试证明:
,试证明: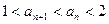 .
.
(本小题满分10分)
过点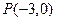 且倾斜角为
且倾斜角为 的直线和曲线
的直线和曲线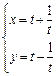 (
(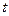 为参数)相交于
为参数)相交于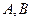 两点.求线段
两点.求线段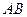 的长.
的长.
本小题满分10分)
已知矩阵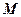
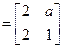 ,其中
,其中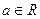 ,若点
,若点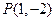 在矩阵
在矩阵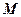 的变换下得到点
的变换下得到点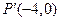 (1)求实数a的值;(2)求矩阵
(1)求实数a的值;(2)求矩阵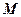 的特征值及其对应的特征向量.
的特征值及其对应的特征向量.
(本小题满分16分)
已知数列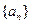 满足
满足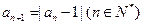 ,(1)若
,(1)若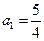 ,求
,求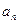 ;
;
(2)是否存在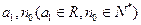 ,使当
,使当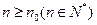 时,
时,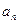 恒为常数。若存在求
恒为常数。若存在求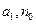 ,否则说明理由;
,否则说明理由;
(3)若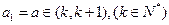 ,求
,求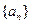 的前
的前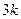 项的和
项的和 (用
(用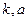 表示)
表示)
本小题满分16分)
如图,已知圆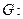
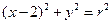 是椭圆
是椭圆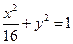 的内接△
的内接△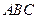 的内切圆, 其中
的内切圆, 其中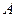 为椭圆的左顶点.
为椭圆的左顶点.
(1)求圆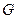 的半径
的半径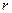 ;
;
( 2)过点
2)过点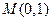 作圆
作圆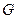 的两条切线交椭圆于
的两条切线交椭圆于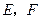 两点,
两点,
|
判断直线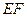 与圆
与圆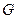 的位置关系并说明理由.
的位置关系并说明理由.
(本小题满分15分)
两县城A和B相距20km,现计划在两县城外以AB为直径的半圆弧 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市 的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在
的的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k ,当垃圾处理厂建在 的中点时,对城A和城B
的中点时,对城A和城B 的总影响度为0.065.
的总影响度为0.065.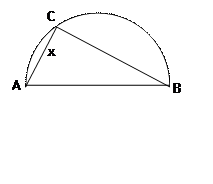
(1)将y表示成x的函数;
(11)讨论(1)中函数的单调性,并判断弧 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由。