等差数列 中,前
中,前 项和为
项和为 ,且
,且 .则
.则 为何值时,
为何值时, 最大?
最大?
(本题12分)已知椭圆C的两焦点分别为F1(﹣1,0)、F2(1,0),短轴的两端点分别为B1、B2,
(1)若椭圆C的离心率为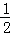 ,直线
,直线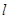 与椭圆相交于A、B两点,弦AB的中点为(
与椭圆相交于A、B两点,弦AB的中点为(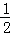 ,1),求直线
,1),求直线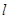 的方程;
的方程;
(2)若椭圆C的短轴长为2,过点F2的直线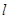 与椭圆C相交于P、Q两点,且
与椭圆C相交于P、Q两点,且 ,求直线
,求直线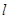 的方程.
的方程.
(本题12分)中国人口已经出现老龄化与少子化并存的结构特征,测算显示中国是世界上人口老龄化速度最快的国家之一,再不实施“放开二胎”新政策,整个社会将会出现一系列的问题.若某地区2015年人口总数为45万,实施 “放开二胎” 新政策后专家估计人口总数将发生如下变化:从2016年开始到2025年每年人口比上年增加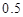 万人,从2026年开始到2035年每年人口为上一年的99%.
万人,从2026年开始到2035年每年人口为上一年的99%.
(1)求实施新政策后第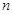 年的人口总数
年的人口总数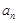 的表达式(注:2016年为第一年);
的表达式(注:2016年为第一年);
(2)若新政策实施后的2016年到2035年人口平均值超过49万,则需调整政策,否则继续实施.问到2035年后是否需要调整政策?(说明: )
)
(本题12分)在锐角 中,
中, 分别为角
分别为角 所对的边,且
所对的边,且
(1)求角 的大小;
的大小;
(2)若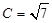 ,且
,且 的面积为
的面积为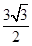 ,求
,求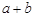 的值.
的值.
(本题12分)已知数列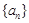 的前
的前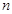 项和
项和 满足
满足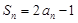
(1)证明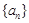 为等比数列,并求
为等比数列,并求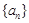 的通项公式;
的通项公式;
(2)设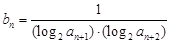 ;求数列
;求数列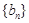 的前
的前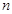 项和
项和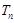 .
.
(本题12分)已知函数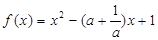 ,
,
(1)当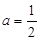 时,解不等式
时,解不等式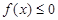 ;
;
(2)比较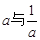 的大小;
的大小;
(3)解关于x的不等式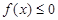 .
.