已知数列{an}中,an=2-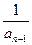 ( n≥2,n∈N+)
( n≥2,n∈N+)
若a1=
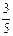 ,数列{bn}满足bn=
,数列{bn}满足bn=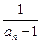 ( n∈N+),求证数列{bn}是等差数列;
( n∈N+),求证数列{bn}是等差数列;
若a1=
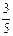 ,求数列{an}中的最大项与最小项,并说明理由.
,求数列{an}中的最大项与最小项,并说明理由.
若1<a1<2, 试证:1<an+1< an<2
设函数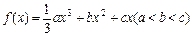 ,其图象在点
,其图象在点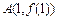 ,
,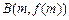 处的切线的斜率分别为
处的切线的斜率分别为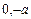
(I)求证: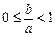 ;
;
(II)若函数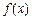 的递增区间为
的递增区间为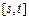 ,求|
,求|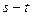 |的取值范围;
|的取值范围;
(III)若当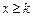 时(
时( 是与
是与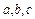 无关的常数),恒有
无关的常数),恒有 ,试求
,试求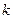 的最小值。
的最小值。
已知函数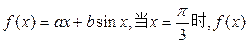 取得极小值
取得极小值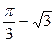 .
.
(Ⅰ)求a,b的值;
(Ⅱ)设直线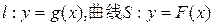 . 若直线l与曲线S同时满足下列两个条件:
. 若直线l与曲线S同时满足下列两个条件:
(1)直线l与曲线S相切且至少有两个切点;
(2)对任意x∈R都有 . 则称直线l为曲线S的“上夹线”.
. 则称直线l为曲线S的“上夹线”.
试证明:直线 是曲线
是曲线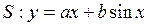 的“上夹线”.
的“上夹线”.
已知函数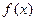 是定义在
是定义在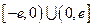 上的奇函数,当
上的奇函数,当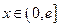 时,
时, 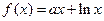 (其中e是自然界对数的底,
(其中e是自然界对数的底, 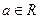 )
)
(1) 求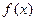 的解析式;
的解析式;
(2) 设 ,求证:当
,求证:当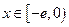 ,
,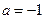 时,
时,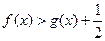 ;
;
(3)是否存在负数a,使得当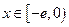 时,
时,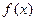 的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
的最小值是3 ?如果存在,求出实数a的值;如果不存在,请说明理由。
(本小题满分16分)设函数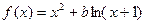 ,其中
,其中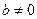 .
.
(1)若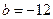 ,求
,求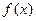 在
在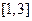 的最小值;
的最小值;
(2)如果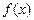 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数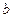 的取值范围;
的取值范围;
(3)是否存在最小的正整数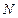 ,使得当
,使得当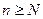 时,不等式
时,不等式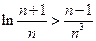 恒成立.
恒成立.
对于函数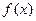 ,若存在
,若存在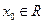 ,使
,使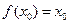 成立,则称
成立,则称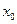 为
为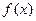 的不动点。如果
的不动点。如果
函数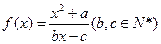 有且仅有两个不动点
有且仅有两个不动点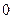 、
、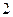 ,且
,且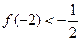 。
。
(1)试求函数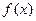 的单调区间;
的单调区间;
(2)点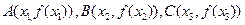 从左到右依次是函数
从左到右依次是函数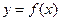 图象上三点,其中
图象上三点,其中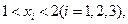 求证:⊿
求证:⊿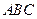 是钝角三角形.
是钝角三角形.