（选做题）从A，B，C，D四个中选做2个，每题10分，共20分．
A．选修4—1 几何证明选讲
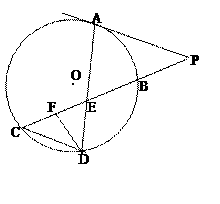如图所示，已知PA与⊙O相切，A为切点，PBC为割线，，弦CD∥AP，AD、BC相交于E点，F为CE上一点，且DE2=EF·EC.
（Ⅰ）求证：ÐP=ÐEDF；
（Ⅱ）求证：CE·EB=EF·EP．
7名同学排队照相．
(1)若分成两排照，前排3人，后排4人，有多少种不同的排法？
(2)若排成两排照，前排3人，后排4人，但其中甲必须在前排，乙必须在后排，有多少种不同的排法？
(3)若排成一排照，甲、乙、丙三人必须相邻，有多少种不同的排法？
(4)若排成一排照，7人中有4名男生，3名女生，女生不能相邻，有多少种不同的排法？
由数字0,1,2,3,4,5可以组成：
(1)多少个没有重复数字的六位偶数；
(2)多少个没有重复数字的比102345大的自然数．
用一颗骰子连掷三次，投掷出的数字顺次排成一个三位数，此时：
(1)各位数字互不相同的三位数有多少个？
(2)可以排出多少个不同的数？
(3)恰好有两个相同数字的三位数共有多少个？
由1、2、3、4四个数字能组成多少个没有重复数字的四位数，试用树形图表示．
求证：An+1m－Anm＝mAnm-1.