设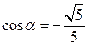 ,
,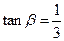 ,
,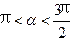 ,
,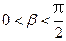 ,求
,求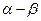 的值.
的值.
某种球的比赛中规定,每次的结果不能出现平局的情况.每赢一次记1分,输一次记0分,先得满20分为赢,赢方可获奖金16万元,现有甲、乙两名水平相当的运动员,当比赛进行到甲、乙两人的积分为17:18时,比赛因某种原因停止,如果按甲、乙两人获胜的概率来分这笔奖金,如何分配这笔奖金?
已知向量
(Ⅰ)当 时,求向量
时,求向量 的夹角
的夹角 ;
;
(Ⅱ)当 时,求函数
时,求函数 的最大值.
的最大值.
已知函数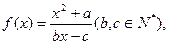 若方程
若方程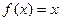 有且只有两个相异实根0,2,且
有且只有两个相异实根0,2,且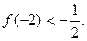
(Ⅰ)求函数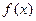 的解析式;
的解析式;
(Ⅱ)已知各项均不为1的数列 满足
满足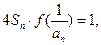 求通项
求通项 ;
;
(Ⅲ)如果数列 满足
满足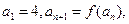 求证:当
求证:当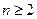 时恒有
时恒有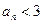 成立.
成立.
在平面直角坐标系中,O为坐标原点,已知点M(1,-3),N(5,1),若点C满足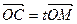
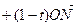 (
(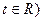 ,点C的轨迹与抛物线
,点C的轨迹与抛物线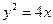 交于A、B两点.
交于A、B两点.
(Ⅰ)求证: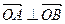 ;
;
(Ⅱ)在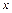 轴正半轴上是否存在一定点P(m,0),使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
轴正半轴上是否存在一定点P(m,0),使得过点P的任意一条抛物线的弦的长度是原点到该弦中点距离的2倍,若存在,求出m的值;若不存在,请说明理由.
已知 是实数,函数
是实数,函数 满足函数
满足函数 在定义域上是偶函数,函数
在定义域上是偶函数,函数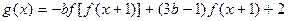 在区间
在区间 上是减函数,且在区间(-2,0)上是增函数.
上是减函数,且在区间(-2,0)上是增函数.
(Ⅰ)求 的值;
的值;
(Ⅱ)如果在区间 上存在函数
上存在函数 满足
满足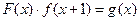 ,当x为何值时,
,当x为何值时, 得最小值.
得最小值.