某种球的比赛中规定,每次的结果不能出现平局的情况.每赢一次记-优题课

某种球的比赛中规定,每次的结果不能出现平局的情况.每赢一次记1分,输一次记0分,先得满20分为赢,赢方可获奖金16万元,现有甲、乙两名水平相当的运动员,当比赛进行到甲、乙两人的积分为17:18时,比赛因某种原因停止,如果按甲、乙两人获胜的概率来分这笔奖金,如何分配这笔奖金?

科目数学题型解答题难度较难

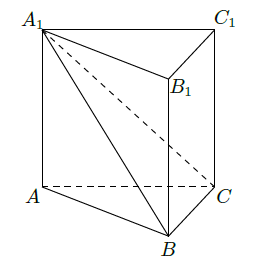
如图，在直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，平面 $A_{1} B C ⊥ 侧面 A_{1} A B B_{1}$ .
（Ⅰ）求证： $A B ⊥ B C$ .

（Ⅱ）若 $A A_{1} = A C = a$ ，直线 $A C$ 与平面 $A_{1} B C$ 所成的角为 $θ$ ，二面角 $A_{1} - B C - A$ 的大小为 $φ$ ，求证： $θ + φ = \frac{π}{2}$ .

已知函数 $f (x) = x^{3} + m x^{2} - m^{2} x + 1$ （ $m$ 为常数，且 $m > 0$ ）有极大值9.
（Ⅰ）求 $m$ 的值；
（Ⅱ）若斜率为-5的直线是曲线 $y = f (x)$ 的切线，求此直线方程.

已知函数 $f (x) = \sin \frac{x}{2} \cos \frac{x}{2} + \cos^{2} \frac{x}{2} - 2$ .

（Ⅰ）将函数 $f (x)$ 化简成 $A \sin (ω x + φ) + B (A > 0, φ > 0, φ \in [0, 2 π))$ 求 $f (x)$ 的周期；

（Ⅱ）求函数 $f (x)$ ;在 $[π, \frac{17 π}{12]}]$ 上的最大值和最小值.

已知数列 ${a_{n}}$ ： $a_{1} = 1, a_{2} = 2, a_{3} = r, a_{n + 3} = a_{n} + 2$ （ $n$ 是正整数），与数列 ${b_{n}}$ ： $b_{1} = 1, b_{2} = 0, b_{3} = - 1, b_{4} = 0, b_{n + 4} = b_{n}$ （ $n$ 是正整数）．记 $T_{n} = b_{1} a_{1} + b_{2} a_{2} + b_{3} a_{3} + . . . + b_{n} a_{n}$ ．
（1）若 $a_{1} + a_{2} + a_{3} + . . . + a_{12} = 64$ ，求 $r$ 的值；
（2）求证：当 $n$ 是正整数时， $T_{128} = - 4 n$ ；
（3）已知 $r > 0$ ，且存在正整数 $m$ ，使得在 $T_{12 m + 1}, T_{12 m + 2}, . . ., T_{12 m + 12}$ 中有4项为100．求 $r$ 的值，并指出哪4项为100．

已知双曲线 $C : \frac{x^{2}}{2} - y^{2} = 1$ ．
（1）求双曲线 $C$ 的渐近线方程；
（2）已知点M的坐标为 $(0, 1)$ ．设 $P$ 是双曲线 $C$ 上的点， $Q$ 是点 $P$ 关于原点的对称点．记 $λ = M P \times M Q$ ．求 $λ$ 的取值范围；
（3）已知点 $D, E, M$ 的坐标分别为 $(- 2, - 1) (2, - 1) (0, 1)$ ， $P$ 为双曲线 $C$ 上在第一象限内的点．记 $l$ 为经过原点与点 $P$ 的直线， $s$ 为 $∆ D E M$ 截直线 $l$ 所得线段的长．试将 $s$ 表示为直线 $l$ 的斜率k的函数．

试卷网试题网古诗词网作文网范文网