已知函数
(
为常数,且
)有极大值9.
(Ⅰ)求
的值;
(Ⅱ)若斜率为-5的直线是曲线
的切线,求此直线方程.
已知函数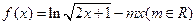 .
.
(1)求函数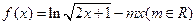 的单调区间;
的单调区间;
(2)若函数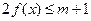 恒成立,求
恒成立,求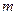 的取值范围.
的取值范围.
已知四棱锥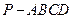 中,
中,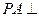 平面
平面 ,底面
,底面 为菱形,
为菱形,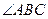 =60
=60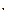 ,
, ,
,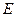 是线段
是线段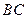 的中点.
的中点.
(1)求证: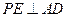 ;
;
(2)求平面 与平面
与平面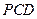 所成锐二面角的大小;
所成锐二面角的大小;
(3)在线段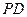 上是否存在一点
上是否存在一点 ,使得
,使得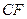 ∥平面PAE,并给出证明.
∥平面PAE,并给出证明.
有甲、乙、丙、丁四名乒乓球运动员,通过对过去战绩的统计,在一场比赛中,甲对乙、丙、丁取胜的概率分别为0.6,0.8,0.9.
(1)若甲和乙之间进行三场比赛,求甲恰好胜两场的概率;
(2)若四名运动员每两人之间进行一场比赛,设甲获胜场次为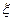 ,求随机变量
,求随机变量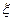 的分布列及数学期望
的分布列及数学期望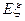 .
.
在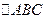 中,角A、B、C所对的边分别是
中,角A、B、C所对的边分别是 ,且
,且 .
.
(1)求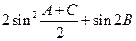 的值;
的值;
(2)若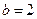 ,求
,求 面积的最大值.
面积的最大值.
(本小题满分15分)
已知函数
 求
求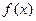 的单调区间;
的单调区间;  若
若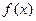 在
在
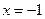 处取得极值,直线
处取得极值,直线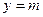 与
与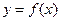 的图象有三个不同的交点,求
的图象有三个不同的交点,求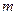 的取值范围。
的取值范围。