已知双曲线
.
(1)求双曲线
的渐近线方程;
(2)已知点M的坐标为
.设
是双曲线
上的点,
是点
关于原点的对称点.记
.求
的取值范围;
(3)已知点
的坐标分别为
,
为双曲线
上在第一象限内的点.记
为经过原点与点
的直线,
为
截直线
所得线段的长.试将
表示为直线
的斜率k的函数.
在边长为 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合于B,构成一个三棱锥(如图所示).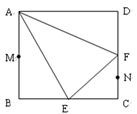
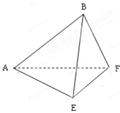
(Ⅰ)在三棱锥上标注出 、
、 点,并判别MN与平面AEF的位置关系,并给出证明;
点,并判别MN与平面AEF的位置关系,并给出证明;
(Ⅱ) 是线段
是线段 上一点,且
上一点,且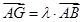 ,问是否存在点
,问是否存在点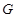 使得
使得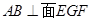 ,若存在,求出
,若存在,求出 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(Ⅲ)求多面体E-AFNM的体积.
已知向量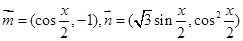 ,设函数
,设函数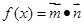 +
+
(1)若 ,f(x)=
,f(x)= ,求
,求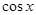 的值;
的值;
(2)在△ABC中,角A,B,C的对边分别是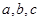 ,且满足
,且满足 ,求f(B)的取值范围.
,求f(B)的取值范围.
设数列 的前
的前 项和为
项和为 ,且
,且
 .
.
(1)证明:数列 是等比数列;
是等比数列;
(2)若数列 满足
满足 ,求数列
,求数列 的前
的前 项和为
项和为 .
.
若a,b,c均为正数,且a+b+c=6,
 对任意x∈R恒成立,求m的取值范围.
对任意x∈R恒成立,求m的取值范围.
已知直线l过点P(2,0),斜率为 直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:(1)|PM|; (2)|AB|.
直线l和抛物线y2=2x相交于A、B两点,设线段AB的中点为M,求:(1)|PM|; (2)|AB|.