已知椭圆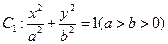 与直线
与直线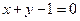 相交于两点
相交于两点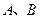 .当椭圆的离心率
.当椭圆的离心率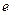 满足
满足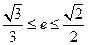 ,且
,且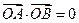 (
(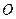 为坐标原点)时,求椭圆长轴长的取值范围.
为坐标原点)时,求椭圆长轴长的取值范围.
设等差数列{an}的公差为d,点(an,bn)在函数f (x)=2x的图象上(n∈N*).
(Ⅰ)证明:数列{bn}为等比数列;
(Ⅱ)若a1=1,直线y=( ln2)(x-a2)+
ln2)(x-a2)+ 在x轴上的截距为2-
在x轴上的截距为2- ,求数列{anb
,求数列{anb }的前n项和Sn.
}的前n项和Sn.
设 的内角
的内角 所对的边长分别为
所对的边长分别为 ,且
,且 ,
, .
.
(Ⅰ)求 及边长
及边长 的值;
的值;
(Ⅱ)若 的面积
的面积 ,求
,求 的周长
的周长 .
.
已知抛物线 与双曲线
与双曲线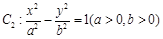 有公共焦点
有公共焦点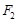 ,点
,点 是曲线
是曲线 在第一象限的交点,且
在第一象限的交点,且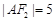 .
.
(Ⅰ)求双曲线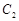 的方程;
的方程;
(Ⅱ)以双曲线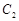 的另一焦点
的另一焦点 为圆心的圆
为圆心的圆 与直线
与直线 相切,圆
相切,圆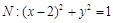 .过点
.过点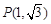 作互相垂直且分别与圆
作互相垂直且分别与圆 、圆
、圆 相交的直线
相交的直线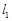 和
和 ,设
,设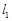 被圆
被圆 截得的弦长为
截得的弦长为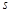 ,
, 被圆
被圆 截得的弦长为
截得的弦长为 ,问:
,问: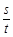 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
如图,在四棱锥 中,侧面PAD⊥底面ABCD,侧棱
中,侧面PAD⊥底面ABCD,侧棱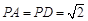 ,
, ,底面
,底面 为直角梯形,其中BC∥AD,AB⊥AD,
为直角梯形,其中BC∥AD,AB⊥AD,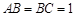 ,O为AD中点.
,O为AD中点.
(Ⅰ)求直线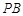 与平面
与平面 所成角的余弦值;
所成角的余弦值;
(Ⅱ)线段 上是否存在一点
上是否存在一点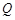 ,使得二面角
,使得二面角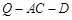 的余弦值为
的余弦值为 ?若存在,求出
?若存在,求出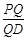 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
从1到9的九个数字中任取三个偶数四个奇数,问:
(Ⅰ)能组成多少个没有重复数字的七位数?
(Ⅱ)上述七位数中三个偶数排在一起的概率?
(Ⅲ)在(Ⅰ)中任意两偶数都不相邻的概率?