某校为进行爱国主义教育,在全校组织了一次有关钓鱼岛历史知识的竞赛.现有甲、乙两队参加钓鱼岛知识竞赛,每队3人,规定每人回答一个问题,答对为本队赢得1分,答错得0分.假设甲队中每人答对的概率均为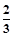 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为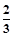 、
、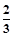 、
、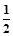 ,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
,且各人回答正确与否相互之间没有影响,用ξ表示甲队的总得分.
(1)求随机变量ξ的分布列和数学期望;
(2)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分” 这一事件,求P(AB).
如图:某污水处理厂要在一个矩形  污水处理池
污水处理池 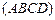 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道 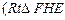 ,
, 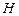
 是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口
是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口 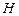 是
是 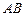 的中
的中  点,
点,  分
分  别落在线段
别落在线段 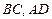 上.已知
上.已知  米,
米, 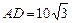 米,记
米,记  .
. 
(Ⅰ)试将污水净化管道的长度  表示为
表示为  的函数
的函数
并写出定义域
(Ⅱ)若 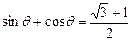 ,求此时管道的长度
,求此时管道的长度 
(Ⅲ)问:当  取何值时,铺设管道的
取何值时,铺设管道的  成本最低?并
成本最低?并  求出此时管道的长度
求出此时管道的长度
已知三次函数 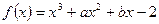 在
在 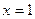 取得极值
取得极值
(Ⅰ)求 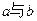 的关系式
的关系式
(Ⅱ)若函数 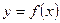 的单调减区间的长度不小于2,
的单调减区间的长度不小于2,  求
求  的取值范
的取值范  围(注:区间
围(注:区间 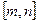 的长度为
的长度为  )
)
(Ⅲ)若不等式  对一切
对一切 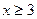 恒成立,求
恒成立,求  的取值范围
的取值范围
在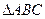 中,
中,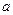 、
、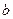 、
、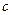 分别为角
分别为角 、
、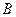 、
、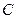 的对边
的对边
已知
(Ⅰ)求角
(Ⅱ)若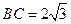 ,内角
,内角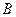 等于
等于 ,周长为
,周长为 ,求
,求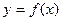 的最大值
的最大值
已知命题  :"
:"  ",命题
",命题  :"
:"  "
"
(Ⅰ)求实数  的取值范围,使命题
的取值范围,使命题  为真命题
为真命题
(Ⅱ)若"  或
或  "是真命题,"
"是真命题,"  且
且  "是假命题,求实数
"是假命题,求实数  的取值范围
的取值范围
已知 .
.
(Ⅰ)求 的值
的值
(Ⅱ)求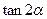 的值
的值