已知三次函数 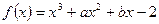 在
在 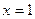 取得极值
取得极值
(Ⅰ)求 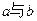 的关系式
的关系式
(Ⅱ)若函数 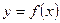 的单调减区间的长度不小于2,
的单调减区间的长度不小于2,  求
求  的取值范
的取值范  围(注:区间
围(注:区间 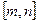 的长度为
的长度为  )
)
(Ⅲ)若不等式  对一切
对一切 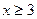 恒成立,求
恒成立,求  的取值范围
的取值范围
A、B两城相距100km,在两地之间距A城 km处D地建一核电站给A、B两城供电,为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数
km处D地建一核电站给A、B两城供电,为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数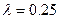 .若A城供电量为20亿度/月,B城为1
.若A城供电量为20亿度/月,B城为1
 0亿度/月.
0亿度/月.
(1)把月供电总费用 表示成
表示成 的函数,并求定义域;
的函数,并求定义域;
(2)核电站建在距A城多远,才能使供电费用最小.
已知函数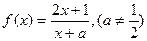 ,
,
(1)若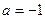 ,证明
,证明 在区间
在区间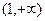 上是增函数;
上是增函数;
(2)若 在区间
在区间
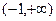 上是单调函数,试求实数
上是单调函数,试求实数 的取值范围。
的取值范围。
已知函数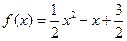
(1)写出函数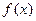 图像的顶点坐标及其单调递增递减区间.
图像的顶点坐标及其单调递增递减区间.
(2)若函数的定义域和值域是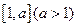 ,求
,求 的值.
的值.
记U=R, 若集合
若集合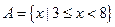 ,
, ,则
,则
(1)求  ,
,  ;
;
(2)若集合 =
= ,
, ,求
,求 的取值范围;
的取值范围;
试比较1.70.2 、log2.1 0.9与0.82.1的大小关系,并按照从小到大的顺序排列为
0.9与0.82.1的大小关系,并按照从小到大的顺序排列为