如图,抛物线的顶点在坐标原点,且开口向右,点A,B,C在抛物线上,△ABC的重心F为抛物线的焦点,直线AB的方程为 。
。
(Ⅰ)求抛物线的方程;
(Ⅱ)设点M为某定点,过点M的动直线l与抛物线相交于P,Q两点,试推断是否存在定点M,使得以线段PQ为直径的圆经过坐标原点?若存在,求点M的坐标;若不存在,说明理由。
已知不等式 的解集为A,不等式
的解集为A,不等式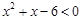 的解集是B.
的解集是B.
(1)求 ;(2)若不等式
;(2)若不等式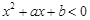 的解集是
的解集是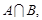 求
求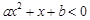 的解集.
的解集.
对某电子元件进行寿命追踪调查,情况如下.
| 寿命(h) |
100~200 |
200~300 |
300~400 |
400~500 |
500~600 |
| 个数 |
20 |
30 |
80 |
40 |
30 |
(1)列出频率分布表; (2)画出频率分布直方图;
(3)估计元件寿命在100~400 h以内的在总体中占的比例;
已知关于x的函数f(x)=-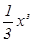 +bx2+cx+bc,其导函数为
+bx2+cx+bc,其导函数为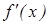 .令g(x)=∣
.令g(x)=∣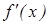 ∣,记函数g(x)在区间[-1、1]上的最大值为M.
∣,记函数g(x)在区间[-1、1]上的最大值为M.
(Ⅰ)如果函数f(x)在x=1处有极值-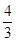 ,试确定b、c的值:
,试确定b、c的值:
(Ⅱ)若∣b∣>1,证明对任意的c,都有M>2:
(Ⅲ)若M≥K对任意的b、c恒成立,试求k的最大值
已知椭圆的中心在坐标原点O,焦点在x轴上,椭圆的短轴端点和焦点所组成的四边形为正方形,两准线间的距离为4
(Ⅰ)求椭圆的方程;
(Ⅱ)直线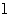 过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.
过点P(0,2)且与椭圆相交于A、B两点,当ΔAOB面积取得最大值时,求直线l的方程.
已知单调递增的等比数列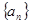 满足:
满足: ,且
,且 是
是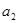 和
和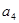 的等差中项.
的等差中项.
(1) 求数列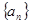 的通项公式
的通项公式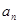 ;
;
(2) 令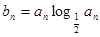 ,
,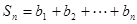 ,求使
,求使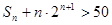 成立的最小的正整数
成立的最小的正整数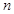 .
.