(本小题14分)已知函数 ,
, (
( 为常数),若直线
为常数),若直线 与
与 和
和 的图象都相切,且
的图象都相切,且 与
与 的图象相切于定点
的图象相切于定点 . (1)求直线
. (1)求直线 的方程及
的方程及 的值;(2)当
的值;(2)当 时,讨论关于
时,讨论关于 的方程
的方程 的实数解的个数.
的实数解的个数.
已知函数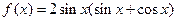
(1)求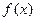 的最小正周期和最大值;
的最小正周期和最大值;
(2)将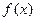 的图像向右平移
的图像向右平移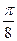 个单位得到函数
个单位得到函数 的图像,求
的图像,求 在
在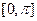 上的零点。
上的零点。
已知函数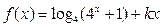
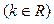 是偶函数[||]
是偶函数[||]
(1) 求 的值;
的值;
(2) 设 ,若函数
,若函数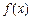 与
与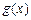 的图象有且只有一个公共点,求实数
的图象有且只有一个公共点,求实数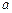 的取值范围。
的取值范围。
在函数 的图象有A、B、C三点,横坐标分别为
的图象有A、B、C三点,横坐标分别为 .
.
(1)若△ABC面积为S,求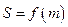 ;
;
(2)求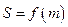 的值域; (3)确定并证明
的值域; (3)确定并证明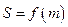 的单调性.
的单调性.
已知幂函数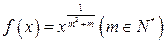
(1)试确定该函数的定义域,并指明该函数在其定义域上的单调性;
(2)若函数还经过 ,试确定
,试确定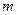 的值,并求满足
的值,并求满足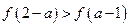 的实数
的实数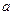 的取值范围。
的取值范围。
某商场经营一批进价是每件30元的商品, 在市场销售中发现此商品的销售单
在市场销售中发现此商品的销售单
价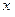 元与日销售量
元与日销售量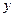 件之间有如下关系:
件之间有如下关系:
销 售单价 售单价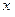 (元) (元) |
30 |
40 |
45 |
50 |
日销售量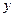 (件) (件) |
60 |
30 |
15 |
0 |
(1)在所给坐标系 中,根据表中提
中,根据表中提 供的数据描出实数对
供的数据描出实数对 对应的点,并确定
对应的点,并确定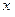 与
与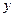 的一个函数关系式
的一个函数关系式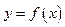 ;
;
(2)设经营此商品的日销售利润为 元,根据上述关系式写出
元,根据上述关系式写出 关于
关于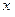 的函数关系式,并指出销售单价
的函数关系式,并指出销售单价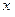 为多少时,才能获得最大日销售利润。
为多少时,才能获得最大日销售利润。