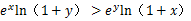某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为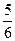 和
和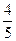 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:至少有1株成活的概率;
两种大树各成活1株的概率
衡阳市八中对参加“社会实践活动”的全体志愿者进行学分考核,因该批志愿者表现良好,学校决定考核只有合格和优秀两个等次.若某志愿者考核为合格,授予1个学分;考核为优秀,授予2个学分,假设该校志愿者甲、乙、丙考核为优秀的概率分别为 、
、 、
、 ,他们考核所得的等次相互独立.
,他们考核所得的等次相互独立.
(1)求在这次考核中,志愿者甲、乙、丙三人中至少有一名考核为优秀的概率;
(2)记在这次考核中甲、乙、丙三名志愿者所得学分之和为随机变量 ,求随机变量
,求随机变量 的分布列及数学期望.
的分布列及数学期望.
已知 ,其中
,其中 ,
, ,
, .
.
(1)求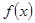 的单调递减区间;
的单调递减区间;
(2)在 中,角
中,角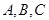 所对的边分别为
所对的边分别为 ,
, ,
, ,且向量
,且向量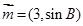 与
与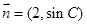 共线,求边长
共线,求边长 和
和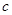 的值.
的值.
已知 是正数组成的数列,
是正数组成的数列,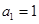 ,且点
,且点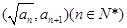 在函数
在函数 的图象上
的图象上
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)若数列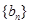 满足
满足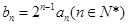 ,求数列
,求数列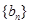 的前
的前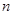 项和.
项和.
为了更好地开展社团活动,丰富同学们的课余生活,现用分层抽样的方法从“模拟联合国”,“街舞”,“动漫”,“话剧”四个社团中抽取若干人组成校社团指导小组,有关数据见下表:(单位:人)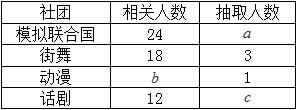
(Ⅰ)求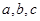 的值;
的值;
(Ⅱ)若从“模拟联合国”与“话剧”社团已抽取的人中选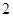 人担任指导小组组长,求这
人担任指导小组组长,求这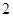 人分别来自这两个社团的概率.
人分别来自这两个社团的概率.
已知函数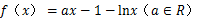
(1)讨论函数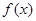 的单调性;
的单调性;
(2)若函数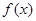 在
在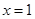 处取得极值,不等式
处取得极值,不等式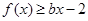 对
对 恒成立,求实数
恒成立,求实数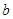 的取值范围;
的取值范围;
(3)当 时,证明不等式.
时,证明不等式.