(本小题满分14分)
在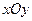 平面上有一系列的点
平面上有一系列的点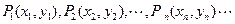 , 对于正整数
, 对于正整数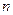 ,点
,点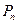 位于函数
位于函数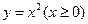 的图像上,以点
的图像上,以点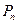 为圆心的
为圆心的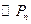 与
与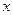 轴相切,且
轴相切,且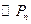 与
与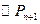 又彼此外切,若
又彼此外切,若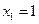 ,且
,且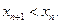
(1)求证:数列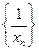 是等差数列;
是等差数列;
(2)设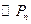 的面积为
的面积为 ,
,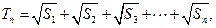 求证:
求证:
根据下列对几何体结构特征的描述,说出几何体的名称.
一个直角梯形绕较长的底边所在的直线旋转一周形成的曲面所围成的几何体.
考古学中常利用死亡的生物体中碳14元素稳定持续衰变的现象测定遗址的年代.假定碳14 每年的衰变率不变,已知它的半衰期为5730年,那么:
(1)碳14的衰变率为多少?
(2)某动物标本中碳14的含量为正常大气中碳14的含量的 (即衰变了
(即衰变了 ),该动物大约在距今多少年前死亡?
),该动物大约在距今多少年前死亡?
在数列 中,设
中,设 .
.
(1)如果 是以
是以 为公差的等差数列,求证
为公差的等差数列,求证 也是等差数列,并求其公差;
也是等差数列,并求其公差;
(2)如果 是以
是以 为公比的等比数列,求证
为公比的等比数列,求证 也是等比数列,并求其公比.
也是等比数列,并求其公比.
已知 是各项均为正数的等比数列,
是各项均为正数的等比数列, 是等比数列吗?为什么?
是等比数列吗?为什么?
图中的三角形称为希尔宾斯基三角形,在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在直角坐标系中画出它的图象.
 |
 |
||||||||||||||
|
|
||||||||||||||
 |
 |
||||||||||||||
|
|||||||||||||||
|
|||||||||||||||