图中的三角形称为希尔宾斯基三角形,在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,请写出这个数列的一个通项公式,并在直角坐标系中画出它的图象.
 |
 |
||||||||||||||
|
|
||||||||||||||
 |
 |
||||||||||||||
|
|||||||||||||||
|
|||||||||||||||
(本小题满分12分)
如图,四棱锥 的底面
的底面 为一直角梯形,其中
为一直角梯形,其中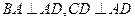 ,
,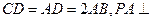 底面
底面 ,
,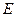 是
是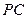 的中点.
的中点.
(1)求证: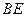 //平面
//平面 ;
;
(2)若 平面
平面 ,求异面直线
,求异面直线 与
与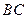 所成角的余弦值;
所成角的余弦值;
(本小题满分12分)
如图,在平行六面体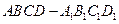 中,
中,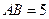 ,
, ,
,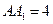 ,
, ,
, ,
,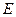 是
是
 的中点,设
的中点,设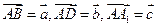 .
.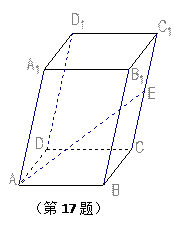
(1)用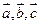 表示
表示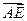
 ;
;
(2)求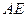 的长.
的长.
(本小题满分12分)
给定两个命题, :对任意实数
:对任意实数 都有
都有 恒成立;
恒成立; :关于
:关于 的方程
的方程 有两个正根;如果
有两个正根;如果 或
或 为真,
为真, 且
且 为假,求实数
为假,求实数 的取值范围.
的取值范围.
(本小题满分12分)已知函数f(x)=ln(x+1)-x.
⑴求函数f(x)的单调递减区间;
⑵若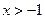 ,证明:
,证明: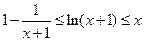 .
.
(本小题满分12分) 已知a为实数,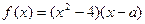 。
。
⑴求导数 ;
;
⑵若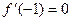 ,求
,求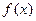 在[-2,2] 上的最大值和最小值;
在[-2,2] 上的最大值和最小值;
⑶若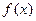 在(-∞,-2)和[2,+∞]上都是递增的,求a的取值范围。
在(-∞,-2)和[2,+∞]上都是递增的,求a的取值范围。