(本小题15分)如图,四棱锥 的底面
的底面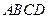 为一直角梯形,其中
为一直角梯形,其中
 ,
, 底面
底面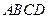 ,
,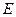 是
是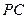 的中点.
的中点.
(1)求证: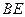 //平面
//平面 ;
;
(2)若 平面
平面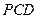 ,
,
①求异面直线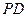 与
与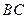 所成角的余弦值;
所成角的余弦值;
②求二面角 的余弦值.
的余弦值.
(本小题14分)已知函数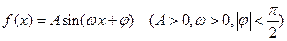 的图像与
的图像与 轴的交点为
轴的交点为 ,它在
,它在 轴右侧的第一个最高点和第一个最低点的坐标分别
轴右侧的第一个最高点和第一个最低点的坐标分别
为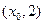 和
和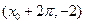 .
.
(1)求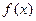 的解析式及
的解析式及 的值;
的值;
(2)若锐角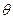 满足
满足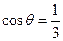 ,求
,求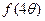 的值.
的值.
(本小题14分)从 这九个数字中任意取出不同的三个数字.
这九个数字中任意取出不同的三个数字.
(1)求取出的这三个数字中最大数字是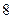 的概率;
的概率;
(2)记取出的这三个数字中奇数的个数为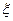 ,求随机变量
,求随机变量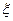 的分布列与数学期望.
的分布列与数学期望.
(本小题15分)已知抛物线 ,过点
,过点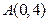 的直线
的直线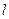 交抛物线
交抛物线 于
于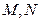 两点,且
两点,且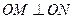 .
.
(1)求抛物线 的方程;
的方程;
(2)过点 作
作 轴的平行线与直线
轴的平行线与直线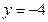 相交于点
相交于点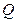 ,若
,若 是等腰三角形,求直线
是等腰三角形,求直线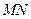 的方程.
的方程.
(本小题15分)已知函数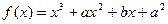 (
(
(1)若函数 在
在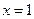 处有极值为
处有极值为 ,求
,求 的值;
的值;
(2)若对任意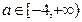 ,
, 在
在 上单调递增,求
上单调递增,求 的最小值.
的最小值.