（本小题满分14分）已知函数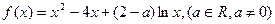
（I）当a=18时，求函数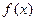
的单调区间；（II）求函数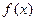在区间
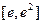上的最小值。
已知
，
，3]．
（1）求f（x）；
（2）求
；
（3）在f（x）与的公共定义域上，解不等式f（x）＞＋
．
设a＞0，函数f（x）＝
-ax在[1，＋∞）上是单调函数．
（1）求实数a的取值范围；
（2）设
≥1，f（x）≥1，且f（f（））＝，求证：f（）＝．
已知函数
（其中
且
）
（I）求函数f(x)的反函数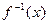
（II）设
，求函数g(x)最小值及相应的x值；
（III）若不等式
对于区间
上的每一个x值都成立，求实数m的取值范围。
如关于
的方程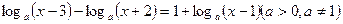
有解，求实数
的取值范围。
对于函数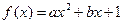
（a＞0），如果方程
有相异两根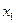
，
．
（1）若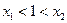
，且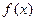
的图象关于直线x＝m对称．求证：
；
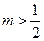（2）若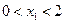
且
，求b的取值范围；
（3）
、
为区间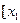
，
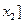上的两个不同的点，求证：
．