一条光线经过P(2,3)点,射在直线l:x+y+1=0上,反射后穿过Q(1,1).
(1)求光线的入射方程;
(2)求这条光线从P到Q的长度.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD, AB//CD,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.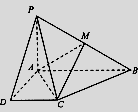
(I)证明:MC//平面PAD;
(II)求直线MC与平面PAC所成角的余弦值.
已知数列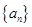 中,
中, ,
,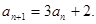
(Ⅰ)记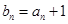 ,求证:数列
,求证:数列 为等比数列;
为等比数列;
(Ⅱ)求数列 的前
的前 项和
项和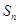
已知函数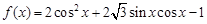
(Ⅰ)求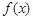 的最小正周期;
的最小正周期;
(Ⅱ)在△ABC中,角A,B,C所对的边分别是 ,
, ,
,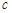 ,若
,若 且
且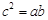 ,
,
试判断△ABC的形状.
某工厂有A、B两种配件生产甲、乙两种产品,每生产一件甲产品使用4个A配件耗时1h,每生产一件乙产品使用4个B配件耗时2h,该厂每天最多可从配件厂获得16个A配件和12个B配件,按每天8h计算,若生产一件甲产品获利2万元,生产一件乙产品获利3万元,采用哪种生产安排利润最大?
已知函数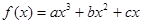 在点
在点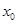 处取得极小值-4,使其导数
处取得极小值-4,使其导数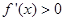 的
的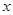 的取值范围为
的取值范围为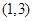 ,求:
,求:
(1)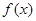 的解析式;
的解析式;
(2) ,求
,求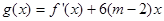 的最大值;
的最大值;