如图,在四棱锥P-ABCD中,PA⊥平面ABCD, AB//CD,∠DAB=90°,PA=AD=DC=1,AB=2,M为PB的中点.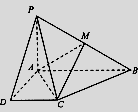
(I)证明:MC//平面PAD;
(II)求直线MC与平面PAC所成角的余弦值.
已知△ABC的内角A、B、C的对边分别为a、b、c,若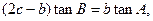 求角A
求角A
(本小题满分 12分)
12分)
已知函数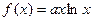 图像上点
图像上点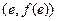 处的切线方程与直线
处的切线方程与直线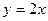 平行(其中
平行(其中 ),
),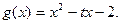
(I)求函数 的解析式;
的解析式;
(II)求函数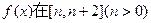 上的最小值;
上的最小值;
(III)对一切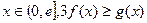 恒成立,求实数t的取值范围.
恒成立,求实数t的取值范围.
(本小题满分12分)
已知椭圆 的焦距为4,且与椭圆
的焦距为4,且与椭圆 有相同的离心率,斜率为
有相同的离心率,斜率为 的直线
的直线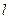 经过点
经过点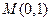 ,与椭圆
,与椭圆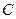 交于不同两点
交于不同两点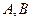 .
.
(Ⅰ)求椭圆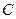 的标准方程;
的标准方程;
(Ⅱ)当椭圆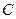 的右焦点
的右焦点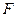 在以
在以 为直径的圆内时,求
为直径的圆内时,求 的取值范围.
的取值范围.
(本小题满分12分)
已知梯形ABCD中,AD∥BC,∠ABC ="∠BAD" =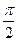 ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF (如图).
(I)当x=2时,求证:BD⊥EG ;
(II)若以F、B、C、D为顶点的三棱锥的体积记为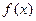 ,
,
求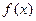 的最大值;
的最大值;
(III)当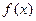 取得最大值时,求二面角D-BF-C的余弦值.
取得最大值时,求二面角D-BF-C的余弦值.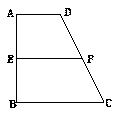
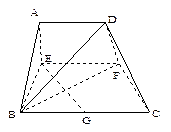 ]
]
(本小题满分12分)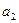 ,
,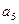 是方程
是方程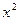
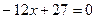 的两根, 数列
的两根, 数列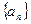 是公差为正的等差数列,数列
是公差为正的等差数列,数列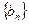 的前
的前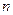 项和为
项和为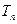 ,且
,且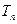
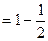
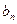
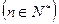 .
.
(I)求数列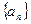 ,
,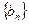 的通项公式; (II)记
的通项公式; (II)记 =
=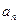
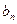 ,求数列
,求数列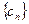 的前
的前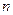 项和
项和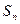 .
.