如图所示，在正方体ABCD—A1B1C1D1中，E、F、G、H分别是BC、CC1、C1D1、A1A的中点.求证：
（1）BF∥HD1；
（2）EG∥平面BB1D1D；
（3）平面BDF∥平面B1D1H.
已知函数f(x)＝ax3＋bx2－3x(a、b∈R)在点x＝－1处取得极大值为2.
(1)求函数f(x)的解析式；
(2)若对于区间[－2，2]上任意两个自变量的值x1、x2，都有|f(x1)－f(x2)|≤c，求实数c的最小值．
设函数f(x)＝(x2＋ax＋b)ex(x∈R)．
(1)若a＝2，b＝－2，求函数f(x)的极大值；
(2)若x＝1是函数f(x)的一个极值点．
①试用a表示b；
②设a＞0，函数g(x)＝(a2＋14)ex＋4.若ξ1、ξ2∈[0，4]，使得|f(ξ1)－g(ξ2)|＜1成立，求a的取值范围．
若函数f(x)＝－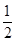
＋blnx在(1，＋∞)上是减函数，求实数b的取值范围．
已知函数f(x)＝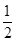
x2－mlnx＋(m－1)x，当m≤0时，试讨论函数f(x)的单调性；
已知函数f(x)＝x3－ax－1.
(1)若a＝3时，求f(x)的单调区间；
(2)若f(x)在实数集R上单调递增，求实数a的取值范围；
(3)是否存在实数a，使f(x)在(－1，1)上单调递减？若存在，求出a的取值范围；若不存在，说明理由．