如图所示,在正方体ABCD—A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q是CC1上的点,问:当点Q在什么位置时,平面D1BQ∥平面PAO?
设数列{an}的前n项和为Sn=2n+1-2,{bn }是公差不为0的等差数列,其中b2、b4、b9依次成等比数列,且a2=b2
(1)求数列{an }和{bn}的通项公式: (2)设cn= ,求数列{cn)的前n项和Tn
,求数列{cn)的前n项和Tn
今年我省取消了省级三好学生、优秀干部、部分体育特长生等高考加分的政策,让广大考生站在一个更公平的平台上竞争,深得社会的广泛好评.但体育确有专长的学生可以通过省里的统一技能测试获得加分,我校今年高三共有5名体育类考生到湖南大学参加体育技能测试,学校指派龙老师带队,已知每位考生测试合格的概率都是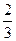 .
.
(1)若他们乘坐的涟源至长沙的汽车恰好有前后两排各3个座位,求龙老师不坐后排的概率;
(2)若5人中恰有r人合格的概率为 ,求r的值.
,求r的值.
如图,正方体ABCD-A1B1C1D1中,E,F分别为AB与BB1的中点,
(Ⅰ)求证:EF⊥平面A1D1B ;
(Ⅱ)求二面角F-DE-C大小.
已知二次函数f(x)的二次项系数为a,且不等式f(x)>2x的解集为(-1,3)
(1)若方程f(x)=-7a有两个相等的实数根,求f(x)的解析式
(2)若函数f(x)在[-2,1]上的最大值为10,求a的值及f(x)在[-2,11]的最小值。
抛物线有光学性质:由其焦点射出的光线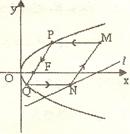 经抛物线反象后,沿平行于抛物线对称轴的肖向射出,反之亦然。
经抛物线反象后,沿平行于抛物线对称轴的肖向射出,反之亦然。
如图所示,今有抛物线C,其顶点是坐标原点,对称辅为x轴。开
口向右。一光源在点M处,由其发出一条平行于x轴的光线射向
抛物线C卜的点P(4.4),经抛物线C反射后,反射光线经过焦点
F后射向抛物线C上的点Q,再经抛物线C反射后又沿平行于X
轴的方向射出,途中经直线l:2x-4y-17=0上点N反射后又射回点M。
(1)求抛物线C的方程;
(2)求PQ的长度;
(3)判断四边形MPQN是否为平行四边形,若是请给出证明,若不是请说明理由。