如图所示,在斜三棱柱A1B1C1—ABC中,底面是等腰三角形,AB=AC,侧面BB1C1C⊥底面ABC.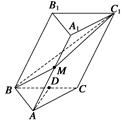
(1)若D是BC的中点.求证:AD⊥CC1;
(2)过侧面BB1C1C的对角线BC1的平面交侧棱于M,若AM=MA1,
求证:截面MBC1⊥侧面BB1C1C.
(本小题满分13分)
在平面直角坐标系中,已知点 ,点
,点 在直线
在直线 上运动,过点
上运动,过点 与
与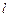 垂直的直线和
垂直的直线和 的中垂线相交于点
的中垂线相交于点 .
.
(Ⅰ)求动点 的轨迹
的轨迹 的方程;
的方程;
(Ⅱ)设点 是轨迹
是轨迹 上的动点,点
上的动点,点 ,
, 在
在 轴上,圆
轴上,圆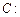
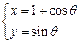 (
( 为参数)内切于
为参数)内切于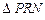 ,求
,求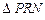 的面积的最小值.
的面积的最小值.
(本小题满分13分)
在一条笔直的工艺流水线上有 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为 ,
, ,
, ,
,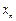 ,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
(Ⅰ)若 ,每个工作台上只有一名工人,试确定供应站的位置;
,每个工作台上只有一名工人,试确定供应站的位置;
(Ⅱ)若 ,工作台从左到右的人数依次为
,工作台从左到右的人数依次为 ,
, ,
, ,
, ,
, ,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
(本小题满分13分)
已知函数 ,
, .
.
(Ⅰ)求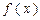 的极值;
的极值;
(Ⅱ)若 在
在 上恒成立,求
上恒成立,求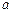 的取值范围.
的取值范围.
(本小题满分12分)
在如图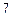 所示的几何体中,
所示的几何体中,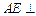 平面
平面 ,
,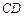 ∥
∥ ,
, 是
是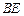 的中点,
的中点,
 ,
, ,
,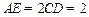 .
.
(Ⅰ)证明 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值.
的余弦值.
图7
(本小题满分12分)
某校在招收体育特长生时,须对报名学生进行三个项目的测试.规定三项都合格者才能录取.假定每项测试相互独立,学生 各项测试合格的概率组成一个公差为
各项测试合格的概率组成一个公差为 的等差数列,且第一项测试不合格的概率超过
的等差数列,且第一项测试不合格的概率超过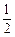 ,第一项测试不合格但第二项测试合格的概率为
,第一项测试不合格但第二项测试合格的概率为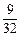 .
.
(Ⅰ)求学生 被录取的概率;
被录取的概率;
(Ⅱ)求学生 测试合格的项数
测试合格的项数 的分布列和数学期望.
的分布列和数学期望.