如图所示，在四棱锥P—ABCD中，底面ABCD为矩形，侧棱PA⊥底面ABCD，AB=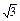
，
BC=1，PA=2，E为PD的中点.
（1）求直线AC与PB所成角的余弦值；
（2）在侧面PAB内找一点N，使NE⊥平面PAC，并求出N点到AB和AP的距离.
已知圆
，直线
．
（Ⅰ）若
与
相切，求
的值；
（Ⅱ）是否存在值，使得与相交于
两点，且
（其中
为坐标原点），若存在，求出，若不存在，请说明理由．
数列
的前
项和记为
（Ⅰ）求的通项公式；
（Ⅱ）等差数列
的各项为正，其前项和为
，且
，又
成等比数列，求
已知等差数列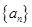
满足：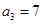
，
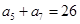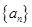，的前n项和为
．
（Ⅰ）求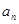
及；
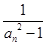（Ⅱ）令bn=
(n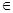
N*)，求数列
的前n项和
．
（本小题满分10分）选修4－5：不等式选修
在
，
的前提下，求a的一个值，是它成为
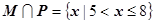的一个充分但不必要条件。
（本小题满分10分）选修4－4：坐标系与参数方程已知曲线C的极坐标方程是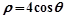
．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是：
（
是参数）.
(1)将曲线C的极坐标方程和直线
参数方程转化为普通方程；
(2)若直线l与曲线C相交于A、B两点，且
，试求实数
值.