已知圆 ,直线
,直线 .
.
(Ⅰ)若 与
与 相切,求
相切,求 的值;
的值;
(Ⅱ)是否存在 值,使得
值,使得 与
与 相交于
相交于 两点,且
两点,且 (其中
(其中 为坐标原点),若存在,求出
为坐标原点),若存在,求出 ,若不存在,请说明理由.
,若不存在,请说明理由.
某商厦欲在春节期间对某新上市商品开展促销活动,经测算该商品的销售量 万件与促销费用
万件与促销费用 万元满足
万元满足 .已知
.已知 万件该商品的进价成本为
万件该商品的进价成本为 万元,商品的销售价格定为
万元,商品的销售价格定为 元/件.
元/件.
(1)将该商品的利润 万元表示为促销费用
万元表示为促销费用 万元的函数;
万元的函数;
(2)促销费用投入多少万元时,商家的利润最大?最大利润为多少?
已知函数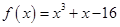 .
.
(1)求曲线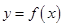 在点
在点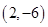 处的切线方程;
处的切线方程;
(2)如果曲线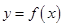 的某一切线与直线
的某一切线与直线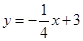 垂直,求切点坐标与切线的方程.
垂直,求切点坐标与切线的方程.
(本小题12分)某村计划建造一个室内面积为800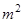 的矩形蔬菜温室.在温室内,沿左.右两侧与后侧内墙各保留1
的矩形蔬菜温室.在温室内,沿左.右两侧与后侧内墙各保留1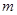 宽的通道,沿前侧内墙保留3
宽的通道,沿前侧内墙保留3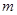 宽的空地.当矩形温室的边长各为多少时?蔬菜的种植面积最大?最大种植面积是多少?
宽的空地.当矩形温室的边长各为多少时?蔬菜的种植面积最大?最大种植面积是多少?
(本小题12分)某企业生产甲、乙两种产品,已知生产每吨甲产品要用A原料3吨,B原料2吨;生产每吨乙产品要用A原料1吨,B原料3吨,销售每吨甲产品可获得利润5万元,每吨乙产品可获得利润3万元.该企业在一个生产周期内消耗A原料不超过13吨,B原料不超过18吨.求该企业获得的最大利润.
(本小题12分)设{an}是等差数列,{bn}是各项都为正数的等比数列,且a1=b1=1,a3+b5=21,a5+b3=13
(Ⅰ)求{an}、{bn}的通项公式;
(Ⅱ)求数列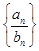 的前n项和Sn.
的前n项和Sn.