设离散型随机变量X的概率分布为
| X |
0 |
1 |
2 |
3 |
4 |
| P |
0.2 |
0.1 |
0.1 |
0.3 |
m |
求:(1)2X+1的概率分布;
(2)|X-1|的概率分布.
已知奇函数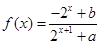 是定义域为
是定义域为 的减函数
的减函数
(Ⅰ)求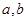 的值;
的值;
(Ⅱ)若对任意的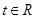 ,不等式
,不等式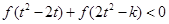 恒成立,求
恒成立,求 的取值范围;
的取值范围;
已知三角形 的顶点坐标为
的顶点坐标为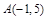 ,
,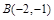 ,
,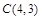 ,
,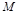 是
是 边上的中点。
边上的中点。
(Ⅰ)求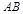 边所在直线的方程;
边所在直线的方程;
(Ⅱ)求中线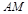 的长;
的长;
(Ⅲ)求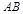 边的高所在直线的方程。
边的高所在直线的方程。
如图,已知在侧棱垂直于底面三棱柱ABC—A1B1C1中,AC=3,AB=5,BC=4,AA1=4,点D是AB的中点.
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求证:AC1∥平面CDB1.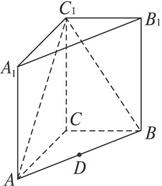
已知直线l经过点P(-2,5),且斜率为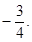
(Ⅰ)求直线l的方程;
(Ⅱ)若直线m与l平行,且点P到直线m的距离为3,求直线m的方程.
已知某几何体的俯视图是如图5所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.
(Ⅰ)求该几何体的体积V;
(Ⅱ)求该几何体的侧面积S.