某地位于甲、乙两条河流的交汇处，根据统计资料预测，今年汛期甲河流发生洪水的概率为0.25，乙河流发生洪水的概率为0.18（假设两河流发生洪水与否互不影响）.现有一台大型设备正在该地工作，为了保护设备，施工部门提 出以下三种方案：
方案1：运走设备，此时需花费4 000元；
方案2：建一保护围墙，需花费1 000元，但围墙只能抵御一个河流发生的洪水，当两河流同时发生洪水时，设备仍将受损，损失约56 000元；
方案3：不采取措施，此时，当两河流都发生洪水时损失达60 000元，只有一条河流发生洪水时，损失为10 000元.
（1）试求方案3中损失费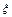
（随机变量）的概率分布；
（2）试比较哪一种方案好.
如图，四边形ABCD内接于圆
，BD是圆的直径，
于点E，DA平分
.
（1）证明：AE是圆的切线；
（2）如果
，
，求CD.
已知函数
，
.
（1）当
时，证明：
；
（2）若
，求k的取值范围.
过抛物线C：
上的点M分别向C的准线和x轴作垂线，两条垂线及C的准线和x轴围成边长为4的正方形，点M在第一象限.
（1）求抛物线C的方程及点M的坐标；
（2）过点M作倾斜角互补的两条直线分别与抛物线C交于A，B两点，且直线AB过点（0，-1），求
的面积.
为了了解高一年级学生的身高情况，某校按10%的比例对全校800名高一年级学生按性别进行抽样检查，得到如下频数分布表：
表1：男生身高频数分布表
| 身高（cm） |
[160,165） |
[165,170） |
[170,175） |
[175,180） |
[180,185） |
[185,190] |
| 频数 |
2 |
5 |
14 |
13 |
4 |
2 |
表2：男生身高频数分布表
| 身高（cm） |
[150,155） |
[150,160） |
[160,165） |
[165,170） |
[170,175） |
[175,180] |
| 频数 |
2 |
12 |
16 |
6 |
3 |
1 |
（1）分别估计高一年级男生和女生的平均身高；
（2）在样本中，从身高180cm以上的男生中任选2人，求至少有一人身高在185cm以上的概率.
在斜三棱柱
中，平面
平面ABC，
，
，
.
（1）求证：
；
（2）若
，求三棱锥
的体积.